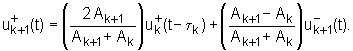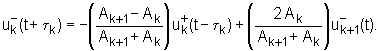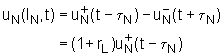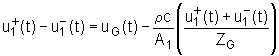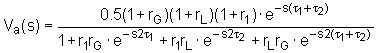1. Akustički govorni model

U prošlom poglavlju diskutirani su osnovni detalji vezani uz akustičku teoriju nastajanja govora. Uz takav detaljni model koji opisuje generiranje (engl. generation), širenje (engl. propagation) i zračenje (engl. radiation) zvuka moguće je u principu odrediti rješenje za izlazni valni oblik govornog signala uz korištenje prikladno odabranih vrijednosti pobude i parametara vokalnog trakta. Primjenom takvih postupaka moguće je izvršiti sintezu govornog signala (umjetni govor), koji će imati vrlo prirodni karakter, tj. zvučat će kao stvarni govorni signal. Međutim, za mnoge je primjene takav detaljan i složeni model nepraktičan i nepotreban. U takvim slučajevima može se koristi jednostavniji pristup modeliranju govornih signala temeljen na akustičkoj teoriji, koji će biti opisan u nastavku.

1.1 Model izvor‑sustav za formiranje govornog signala

Slika 6.1‑1 prikazuje poopćeni blok dijagram nastajanja govora, koji predstavlja osnovu velikog broja modela korištenih za obradbu ili analizu govora. Svim je ovim modelima zajedničko da je pobuda odijeljena od vokalnog trakta i svojstava zračenja. Utjecaji vokalnog trakta i zračenja ujedinjeni su u vremenski promjenjivom linearnom sustavu čija je namjena modeliranje rezonantnih karakteristika opisanih u prošlom poglavlju.

Slika

6.1‑1

Model “izvor-sustav” kod stvaranja govora

Generator pobudnog signala na svom izlazu ima ili niz pulseva (tzv. glotalnih pulseva), ili slučajno promjenjivi signal (šum). Parametri izvora i sustava su tako odabrani da rezultirajući izlazni signal ima željene karakteristike koje su što sličnije prirodnom govoru. Ako je to ostvarivo, opisani model može poslužiti kao temelj za obradbu govora. U narednim poglavljima biti će opisani modeli koji se temelje na upravo opisanom principu.

1.2 Model sa spojenim cijevima bez gubitaka

Vrlo široko upotrebljavan model formiranja govora temeljen je ne pretpostavci da se vokalni trakt u određenom trenutku vremena može opisati pomoću niza međusobno spojenih cijevi bez gubitaka, kao što je prikazano na slici 6.2‑1. Svaka od tih cijevi ima stalan poprečni presjek Ak i dužinu lk. Površine poprečnog presjeka cijevi i njihove dužine odabrane su tako da aproksimiraju funkciju površine poprečnog presjeka vokalnog trakta, A(x). Ako se koristi mnogo kratkih cijevi, može se očekivati da će rezonantne frekvencije (formanti) spojenih uniformnih cijevi biti bliske onima kod cijevi s kontinuirano promjenjivom funkcijom površine poprečnog presjeka, A(x). Međutim, budući da ova aproksimacija zanemaruje gubitke uslijed trenja, toplinske vodljivosti i vibracije stjenki cijevi, može se očekivati da će se širine frekvencijskih pojaseva formanata ovog pojednostavljenog modela razlikovati od širina kod detaljnog modela koji uključuje spomenute gubitke. Neke od tih gubitaka je ipak moguće uzeti u obzir i kod ovog modela, a radi se o utjecaju glotalne impedancije na početku prve cijevi, kao i utjecaju impedancije zračenja na kraju zadnje cijevi, čime se povećava točnost aproksimacije takvog modela.

Slika

6.2‑1

Model vokalnog trakta sa spojenim cijevima bez gubitaka:
 a) izgled modela, b) pojednostavljena skica

 

Za sadašnju raspravu, mnogo je važnija činjenica da modeli sa cijevima bez gubitaka omogućuju pogodniji prijelaz s vremenski kontinuiranih modela na vremenski diskretne. Prema tome, u nastavku će se razmatrat upravo modeli oblika poput onog sa slike 6.2‑1.

1.3 Širenje zvučnih valova u spojenim cijevima

Budući da cijevi sa slike 6.2‑1 prema pretpostavci nemaju gubitaka, širenje zvuka kroz
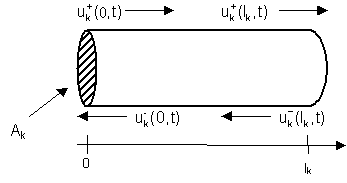
k-tu cijev prikazanu na slici 6.3‑1 s površinom poprečnog presjeka  i dužinu lk može biti opisano slijedećim relacijama za tlak i brzinu protoka volumena zraka:

Slika

6.3‑1

k-ta cijev bez gubitaka

 

(6.3‑1)

(6.3‑2)

gdje x predstavlja udaljenost od lijevog kraja k-te cijevi (0 £ x £ lk) (slika 6.3‑1), a  su pozitivno odnosno negativno putujući val kroz k-tu cijev.

Odnos između putujućih valova u susjednim cijevima možemo odrediti primjenom fizikalnog principa da tlak i brzina protoka volumena zraka moraju biti kontinuirani i u prostoru i vremenu svugdje u sustavu. Iz ovoga slijede granični uvjeti, koji se primjenjuju na oba kraja cijevi.

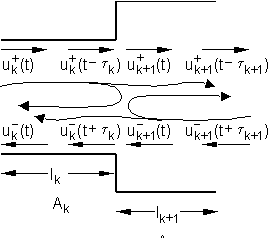
Ako se razmotri spoj između k-te i (k+1)-ve cijevi, kao što je prikazano na slici 6.3‑2, primjenom uvjeta kontinuiteta na spoju cijevi, dobiva se:

(6.3‑3)

(6.3‑4)

Uvrštavanjem jednadžbi (6.3‑1) i (6.3‑2) u jednadžbe (6.3‑3) i (6.3‑4), dobiva se:

(6.3‑5)

(6.3‑6)

gdje jevrijeme potrebno za prolazak zvučnog vala kroz k-tu cijev. Iz slike 6.3‑2 može se uočiti da se dio vala koji se širi kroz k-tu cijev u pozitivnom smjeru, kada dosegne rub cijevi djelomično prenosi dalje na desno, dok se dio reflektira (na lijevo).

Slika

6.3‑2

Ilustracija spoja između dvije cijevi bez gubitaka

Slično tomu, val koji ide u negativnom smjeru kroz (k+1)-vu cijev dijelom se prenosi na lijevo u k-tu cijev, dok se dio ponovno reflektira nazad u desno. Ako se  izraze preko  moći će se odrediti ponašanje originalnog i reflektiranog vala u cijelom sustavu. Ako se iz jednadžbe (6.3‑6) izrazi i uvrsti u jednadžbu (6.3‑5), dobiva se slijedeći izraz:

(6.3‑7)

Oduzimanjem jednadžbe (6.3‑6) od jednadžbe (6.3‑5), slijedi izraz:

(6.3‑8)

Iz jednadžbe (6.3‑7) može se zaključiti da veličina

(6.3‑9)

određuje koliki dio negativno putujućeg vala  se reflektira na granici dviju cijevi. Zbog toga se veličina rk naziva faktorom refleksije za k-ti spoj (spoj k-te i (k+1)-ve cijevi). S obzirom da su sve površine poprečnih presjeka pozitivne veličine, lako se pokazuje da vrijedi:

(6.3‑10)

Koristeći se definicijom faktora refleksije rk iz izraza (6.3‑9) moguće je jednadžbe (6.3‑7) i (6.3‑8) zapisati u slijedećem obliku:

(6.3‑11)

(6.3‑12)

Ove jednadžbe mogu se prikazati i grafički pomoću blok dijagrama na slici 6.3‑3. Operacije množenja i zbrajanja u jednadžbama (6.3‑11) i (6.3‑12), prikazane su u blok dijagramu prema konvencijama za grafove toka signala za prikaz množenja i zbrajanja. Jasno je da se svaki spoj dvije susjedne cijevi modela vokalnog trakta prikazanog na slici 6.2‑1, može prikazati sustavom poput onog na slici 6.3‑3. Ovakav model nam daje rješenje za tlak i brzinu protoka na rubovima svakog segmenta. Ta činjenica ne predstavlja ograničenje budući da je najzanimljiviji odnos upravo onaj između izlaza zadnje cijevi i ulaza prve cijevi. Tako će npr. model s pet cijevi bez gubitaka prikazan na slici 6.2‑1, imati pet grupa unaprednih (engl. forward) i unazadnih (engl. backward) kašnjenja i četiri spoja, svaki opisan svojim faktorom refleksije.

Slika

6.3‑3

Spoj između dvije cijevi bez gubitaka prikazan pomoću grafa toka signala

Radi potpunog opisa ovog modela potrebno je diskutirati i rubne uvjete na prvom odnosno zadnjem segmentu sustava, kao što će biti prikazano u slijedećem poglavlju.

1.4 Rubni uvjeti modela sa spojenim cijevima bez gubitaka

Pretpostavimo da se model vokalnog trakta sastoji od N cijevi (segmenata) označenih brojevima 1 do N, gdje početak prve cijevi odgovara glasnicama, dok kraj N-te cijevi odgovara usnicama. U tom slučaju će rubni uvjet na usnicama određivati odnos između tlaka pN(lN,t) i brzine protoka uN(lN,t) na izlazu N-te cijevi, sa tlakom i brzinom protoka na početku otvorenog prostora kroz koji se zvučni val širi zračenjem s usnica.

Prije je već pokazano, da su u slučaju pobude s kompleksnom eksponencijalnom, kompleksna amplituda tlaka i brzine protoka volumena zraka na usnicama povezane s impedancijom zračenja ZL, tj. prema izrazu:

(6.4‑1)

Ako za prvu ruku ignoriramo činjenicu da je ZL kompleksna veličina i pretpostavimo da je realna, tada se izraz (6.4‑1) može u vremenskoj domeni napisati kao:

(6.4‑2)

Ako iz ovog izraza izrazimo  kao funkciju od , tada slijedi:

(6.4‑3)

gdje je faktor refleksije na usnicama rL definiran slijedećim izrazom:

(6.4‑4)

Prema tome brzina protoka na ulazu u otvoreni prostor uN(lN,t) odgovara razlici između pozitivno putujućeg vala  i njegove reflektirane vrijednosti , tj. prema:

(6.4‑5)

Opisana pojava refleksije na kraju zadnje cijevi određena gornjim izrazima ilustrirana je i grafički na slici 6.4‑1.

Slika

6.4‑1

Rubni uvjet na usnicama (spoj zadnje cijevi i slobodnog prostora)

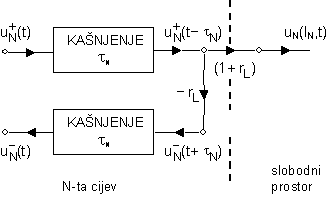
U slučaju da je zaključna impedancija ZL kompleksan broj (što i jest istina), može se pokazati da tada i dalje vrijedi izraz (6.4‑4) za faktor refleksije rL, jedino što je tada i on kompleksan broj. U tom slučaju se izraz (6.4‑3) mora zapisati u frekvencijskoj domeni, što vodi na diferencijalnu jednadžbu koja povezuje  i .

Analiza za rubni uvjet na glasnicama je vrlo slična prethodnom slučaju. Uz pretpostavku da se pobudni signal može odvojiti od vokalnog trakta, tj. modelirati kao paralelni spoj idealnog strujnog izvora uG(t) i glotalne impedancije ZG koji su spojeni na ulaz prve cijevi kao što je prikazano na slici 5.5‑5, tada su prema izrazu (5.5‑2) tlak i brzina protoka na ulazu u prvu cijev u frekvencijskoj domeni vezani slijedećim izrazom:

(6.4‑6)

Ako ponovno pretpostavimo da je impedancija ZG realna, tada se dobiva slijedeći izraz u vremenskoj domeni:

(6.4‑7)

Ako izrazimo  kao funkciju od  i pobude uG(t) , tada slijedi:

(6.4‑8)

gdje je faktor refleksije na glasnicama rG definiran slijedećim izrazom:

(6.4‑9)

Odnosi opisani jednadžbama (6.4‑8) i (6.4‑9) mogu se predočiti i grafički, kao što je prikazano na slici 6.4‑2.

Slika

6.4‑2

Rubni uvjet na glasnicama (spoj glasnica i prve cijevi )

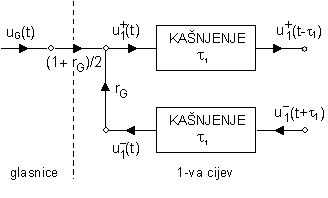
Analogno kao i kod rubnog uvjeta na usnicama i ovdje izraz (6.4‑9) za faktor refleksije rG vrijedi čak i za kompleksnu glotalnu impedanciju ZG. U tom slučaju se izraz (6.4‑8) mora zapisati u frekvencijskog domeni, što vodi na diferencijalnu jednadžbu koja povezuje  sa  i uG(t).

Sada kada su poznati svi elementi ovog modela, moguće je ilustrirati cjelokupni sustav na primjeru sustava s dvije spojene cijevi, kao što je prikazano na slici 6.4‑3.

Slika

6.4‑3

Ukupni model za sustav s dvije spojene cijevi

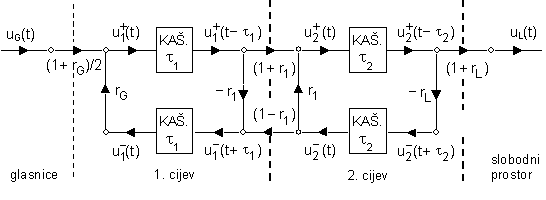
Izlaz tog modela predstavlja brzina protoka volumena zraka na usnicama uL(t)=u2(l2,t), dok je ulaz pobudni signal uG(t). U slučaju pobudnog signala oblika kompleksne eksponencijale moguće je odrediti frekvencijsku karakteristiku cijelog sustava, tj. omjer kompleksne amplitude brzine protoka na izlazu UL(W) i amplitude na ulazu UG(W). Raspisivanjem svih izraza opisanih u prethodnim poglavljima u frekvencijskoj domeni, frekvencijska karakteristika dvocijevnog sustava se nalazi kao:

(6.4‑10)

Potrebno je uočiti da član  koji se javlja u brojniku ove frekvencijske karakteristike pomnožen s konstantom predstavlja kašnjenje cjelokupnog sustava od glasnica do usnica u iznosu od (t1+t2). Ova frekvencijska karakteristika se može transformirati u prijenosnu funkciju sustava Va(s) jednostavnom zamjenom jW sa s, kao što slijedi:

(6.4‑11)

Polovi prijenosne funkcije Va(s) određuju rezonantne karakteristike modela sa spojenim cijevima bez gubitaka. Nazivnik ove funkcije je malo neobičan, tj. umjesto da se u nazivniku nalazi običan polinom u varijabli s čije korijene je lako naći, kompleksna frekvencija s se javlja u eksponentu. Poznato je da se eksponencijalna funkcija može raspisati kao beskonačni red potencija , što drugim riječima znači da je polinom u nazivniku beskonačnog stupnja i da ima beskonačno mnogo korijena. Međutim, pokazalo se da se uz pogodno odabrane dužine segmenata i njihove poprečne presjeke dobiva prijenosna funkcija Va(s) koja dobro aproksimira stvarnu akustičku prijenosnu funkciju za veći broj samoglasnika.