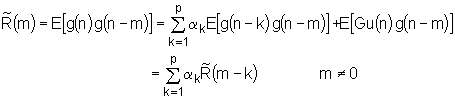1.1 Faktor pojačanja LPC filtra

Razumno je očekivati da se iznos pojačanja G može odrediti usporedbom energije signala s energijom linearno predviđenih uzoraka. Ta tvrdnja je doista istinita ako se za signal pobude LPC sustava uvedu odgovarajuće pretpostavke.

Koristeći jednadžbe (9.3‑3) i (9.3‑5) moguće je povezati faktor pojačanja G sa signalom pobude i pogreškom predikcije. Signal pobude može se izraziti kao:

(9.6‑1)

dok se signal predikcijske pogreške, e(n) može izraziti kao:

(9.6‑2)

U slučaju jednakosti koeficijenata prediktora i koeficijenata modela vokalnog trakta, to jest za , vrijedi:

(9.6‑3)

odnosno, ulazni signal je proporcionalan signalu pogreške predikcije, a konstanta proporcionalnosti je faktor pojačanja G.

Jednadžba (9.6‑3) je samo približna (to jest, vrijedi samo u slučaju jednakosti idealnih i stvarnih parametara linearnog prediktora), pa općenito nije moguće pouzdano izraziti G direktno preko signala pogreške. Zbog toga se uvodi jednostavna pretpostavka koja samo zahtjeva da energija signala pogreške bude jednaka energiji signala pobude, to jest:

(9.6‑4)

Da bi bilo moguće povezati faktor pojačanja G s poznatim veličinama: koeficijentimai korelacijskim koeficijentima, potrebno je uvesti neke pretpostavke o signalu pobude u(n). Interesantna su dva slučaja pobude. Za zvučni govor u slučaju kada se analiza provodi sinkrono s glotalnim pulsevima i to tako da je točno jedan osnovni period titranja glasnica sadržan unutar okvira analize, tada se može pretpostaviti da je , to jest pobuda je jedinični uzorak u koraku . Da bi ta pretpostavka bila valjana, spektralna svojstva valnog oblika glotalnog pulsa zvučnog govora moraju biti integrirana u cjelokupni model vokalnog sustava , tj. oba utjecaja(valni oblik pobudnog signala i frekvencijska karakteristika vokalnog trakta) se modeliraju vremenski promjenjivim sustavom . To zahtjeva da red prediktora, p, bude dovoljno visok da obuhvati efekte vokalnog trakta i glasnica. Za bezvučni govor najbolje je pretpostaviti da je stacionaran bijeli šum, srednje vrijednosti jednake nuli i jedinične varijance.

Na osnovi ovih pretpostavki i koristeći jednadžbu (9.6‑4) možemo odrediti faktor pojačanja G. Za zvučni govor pobuda sustava je jednaka , pa je stoga odziv na tu pobudu jednak impulsnom odzivu tog sustava h(n), odnosno vrijedi:

(9.6‑5)

Može se pokazati da autokorelacijska funkcija impulsnog odziva h(n) definirana kao:

(9.6‑6)

zadovoljava jednadžbe:

m=1, 2, ... , p

(9.6‑7)

i

(9.6‑8)

Obzirom da su jednadžbe (9.6‑7) i (9.6‑8) identične jednadžbi (9.4‑9), slijedi da:

(9.6‑9)

Ukupna energija u signalu R(0) i impulsnom odzivu mora biti jednaka, pa se korištenjem jednadžbi (9.4‑10), (9.6‑4), i (9.6‑8) dobiva:

(9.6‑10)

Interesantno je primijetiti da jednadžba (9.6‑9), kao i zahtjev da energije impulsnog odziva i signala budu jednake, zapravo zajedno zahtijevaju da prvih p+1 koeficijenata autokorelacijske funkcije impulsnog odziva modela budu identični prvim p+1 koeficijentima autokorelacijske funkcije signala govora.

U slučaju bezvučnog govora, korelacijske funkcije su definirane kao statistička očekivanja. Pretpostavlja se da je na ulazu sustava bijeli šum, srednje vrijednosti nula i jedinične varijance, to jest:

(9.6‑11)

Ako se sustav pobudi slučajnim signalom , a odziv sustava se nazove , tada je

(9.6‑12)

Ako označava autokorelacijsku funkciju signala , tada je

(9.6‑13)

jer je za zbog nekoreliranosti s nijednim signalom koji prethodi . Za dobije se:

(9.6‑14)

jer je . Pošto energija odziva na pobudu mora biti jednaka energiji signala, dobije se:

(9.6‑15)

ili

(9.6‑16)

tj. isto kao što je bio u slučaju impulsne pobude zvučnog govora.