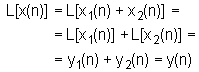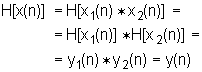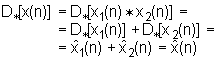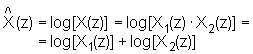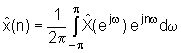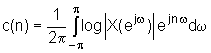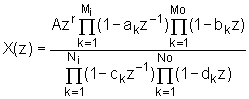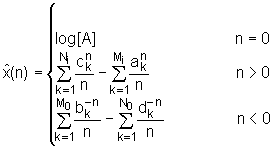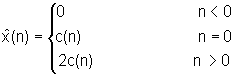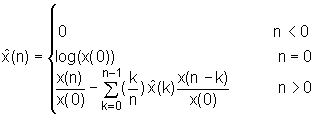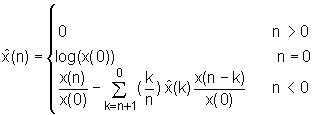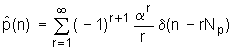1. Homomorfna obrada govornog signala

1.1 Uvod

Jedna od osnovnih pretpostavki vezana uz obradu govornog signala je da se govor može prikazati kao izlaz iz linearnog, vremenski promjenljivog sustava čija se svojstva sporo mijenjaju s vremenom. To vodi prema osnovnom principu analize govora koji kaže da ako se promatraju dovoljno kratki segmenti govornog signala, da se tada svaki segment može učinkovito modelirati kao izlaz iz linearnog, vremenski invarijantnog sustava pobuđenog bilo kvazi-periodičnim impulsima bilo slučajnim šumom (engl. random noise signal). Problem govorne analize predstavlja određivanje parametara govornog modela kao i određivanje njihovih promjena u vremenu. Pošto konvolucija pobude i impulsnog odziva linearnog, vremenski invarijantnog sustava predstavlja njegov izlaz (govorni signal), ovaj se problem može promatrati i kao problem razdvajanja konvolviranih komponenti, što je poznato pod nazivom dekonvolucija. Dekonvolucija se može razmatrati sa stanovišta vremenski kratkotrajne Fourier-ove analize, ali i korištenjem koncepta homomorfne filtracije, što će biti objašnjeno u nastavku.

1.2 Sustavi homomorfni za konvoluciju

Homomorfni sustavi za konvoluciju podliježu općem principu superpozicije. Ovaj se princip za uobičajene linearne sustave izražava sljedećim uvjetima:

(10.2‑1)

 

gdje je L linearni operator. Princip superpozicije kaže da ukoliko je ulazni signal sastavljen od linearne kombinacije elementarnih signala, tada je izlaz linearna kombinacija pripadnih izlaza linearnog operatora za svaki od tih ulaza. To je prikazano slikom 10.2‑1 gdje simbol + na ulazu i izlazu bloka L[ ] označava da aditivna kombinacija na ulazu proizvodi aditivnu kombinaciju na izlazu.

Slika

10.2‑1

Prikaz sustava koji zadovoljava princip superpozicije

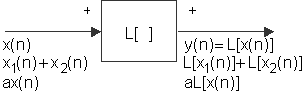
Vrlo dobar primjer primjene principa superpozicije je izraz za konvoluciju gdje se odziv linearnog sustava na pobudu x(n) nalazi kao superpozicija pomaknutih i skaliranih impulsnih odziva h(n) prema izrazu:

(10.2‑2)

Simbol * će u nastavku označavati operaciju vremenski diskretne linearne konvolucije. Po analogiji s principom superpozicije za obične linearne sustave može se definirati grupa sustava H[ ] koja podliježe općem principu superpozicije kod kojeg je zbrajanje zamijenjeno operacijom konvolucije (može se lako pokazati da konvolucija ima ista algebarska svojstva kao i zbrajanje). Takvi sustavi moraju zadovoljavati slijedeći uvjet:

(10.2‑3)

Oni bi morali zadovoljavati i dugo svojstvo principa superpozicije, tj. množenje s konstantom, ali to svojstvo nije značajno za primjene koje će se razmatrati u nastavku.

Sustavi koji imaju svojstvo dano izrazom (10.2‑3) nazivaju se sustavi homomorfni za konvoluciju. Porijeklo ovakvog naziva dolazi iz činjenice da se ovakva transformacija može prikazati kao homomorfna transformacija u smislu linearnog vektorskog prostora. Primjer takvog sustava prikazan je slikom 10.2‑2, gdje je operacija konvolucije * označena eksplicitno na ulazu i na izlazu iz sustava.

Slika

10.2‑2

Prikaz sustava homomorfnog za konvoluciju

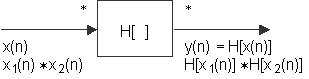
Homomorfni filtar je u osnovi homomorfni sustav koji ima svojstvo da jedna (željena) komponenta prolazi kroz sustav nepromijenjena, dok je neželjena komponenta odstranjena. Npr., ako je u izrazu (10.2‑3) neželjena komponenta , može se zahtijevati da izlaz H[x1(n)] koji odgovara ulazu  bude jedinični uzorak, dok izlaz H[x2(n)] koji odgovara ulazu  bude što bolja aproksimacija . Tada će konvolucija ta dva izlazna signala biti jednaka H[x2(n)] čime je odvojena samo željena komponenta. Ovo je u potpunosti analogno situaciji kod običnih linearnih sustava, gdje se pojavljuje problem razdvajanja željenog signala iz aditivne kombinacije signala i šuma.

Važan aspekt teorije homomorfnih sustava je da se bilo koji takav sustav može prikazati kao kaskada tri homomorfna sustava kao što je predočeno slikom 10.2‑3 za slučaj sustava homomorfnog za konvoluciju.

Slika

10.2‑3

Kaskadni oblik sustava za homomorfnu dekonvoluciju

U prvi sustav ulazi signal koji predstavlja konvoluciju dvije komponente i transformira se u aditivnu kombinaciju odgovarajućih izlaza. Drugi sustav je uobičajeni linearni sustav koji podliježe principu superpozicije iskazanom izrazima (10.2‑1). Treći sustav je inverzan prvom, što znači da transformira aditivnu kombinaciju signala nazad u konvolucijsku kombinaciju izlaza. Prednost ovakvog kaskadnog rastava homomorfnih sustava je u činjenici da je karakteristika ukupnog sustava određena središnjim linearnim sustavom koji se projektira za željenu primjenu. Suprotno tome sustav  koji se naziva karakteristični sustav za homomorfnu dekonvoluciju se ne mijenja (uvijek je jednak), a podliježe generaliziranom principu superpozicije gdje je ulazna operacija konvolucija, a izlazna operacija obično zbrajanje. Svojstva karakterističnog sustava su definirana na sljedeći način:

(10.2‑4)

Isto tako, inverzni karakteristični sustav  je također fiksan sustav, a definiran na sljedeći način:

(10.2‑5)

Za određivanje karakterističnog sustava za dekonvoluciju potrebno je krenuti od ulaznog signala x(n) koji predstavlja konvoluciju signala x1(n) i x2(n):

(10.2‑6)

Taj signal moguće je prikazati i u z-domeni kao produkt z-transformacija ulaznih signala:

(10.2‑7)

Slika

10.2‑4

Prikaz sustava homomorfnog za konvoluciju u frekvencijskoj domeni

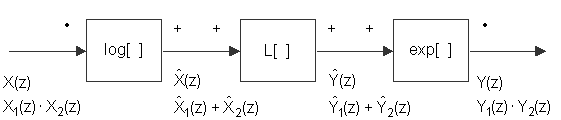
Iz izraza (10.2‑4) proizlazi da z-transformacija izlaza karakterističnog sustava mora biti aditivna kombinacija dvaju z-transformacija. Prema tome, karakteristični sustav za dekonvoluciju u frekvencijskoj domeni mora imati svojstvo da ukoliko je ulazni signal produkt z-transformacija, tada izlaz mora biti zbroj transformiranih ulaza. Jedna mogućnost realizacije takvog sustava prikazana je na slici 10.2‑4. Ona se temelji na činjenici da se logaritam produkta može prikazati kao zbroj logaritama množitelja, tj.:

(10.2‑8)

Ukoliko želimo prikazati signale u obliku vremenskih nizova, umjesto njihove reprezentacije u frekvencijskoj domeni kao na slici 10.2‑4, karakteristični sustav se može prikazati kao što je učinjeno na slici 10.2‑5. Slično tome, inverzni karakteristični sustav može se prikazati slikom 10.2‑6.

Slika

10.2‑5

Prikaz karakterističnog sustava za homomorfnu

dekonvoluciju

Slika

10.2‑6

Prikaz inverznog karakterističnog sustava za homomorfnu dekonvoluciju

Ova dva prikaza temeljeni su na valjanosti izraza (10.2‑8), tj. logaritam mora biti definiran tako da vrijedi da je logaritam produkta jednak sumi logaritama. To je trivijalno za realne pozitivne veličine, međutim, Z-transformacija je u osnovi kompleksna veličina te se postavlja pitanje jednoznačnosti logaritma kompleksnog broja. Pošto se u stvarnim aplikacijama umjesto Z-transformacije koristi Fourier‑ova transformacija, tj. Z-transformacija se promatra samo za vrijednosti na jediničnoj kružnici (za ), dovoljno je osigurati da izraz (10.2‑8) vrijedi u tim uvjetima. U tom slučaju se kompleksni logaritam može definirati kao:

(10.2‑9)

Iako je u ovom izrazu korišten prirodni logaritam, može se koristiti logaritam po bilo kojoj drugoj bazi. S realnim dijelom nema nekih osobitih poteškoća, dok se problemi jednoznačnosti pojavljuju pri definiranju imaginarnog dijela, koji je jednak kutu Z-transformacije na jediničnoj kružnici. Jedan od pristupa ovom problemu je zahtjev da fazni kut bude kontinuirana neparna funkcija od , čime je zadovoljen izraz (10.2‑8). Naime fazni kut u izrazu (10.2‑9) se mijenja u intervalu od ‑p do p, tj. postoje lomovi i višeznačnost funkcije pa se tako definiran logaritam ne može direktno primijeniti. Rješenje problema se može postići postupkom nadopunjavanja osnovne vrijednosti faze (npr. ‑p do p) cjelobrojnim višekratnicima od 2p. To znači da na svim mjestima gdje faza ima diskontinuitet reda veličine 2p, potrebno je pribrojiti cjelobrojni višekratnik od 2p koji osigurava kontinuiranost funkcije faze. Treba također osigurati da i na početku (w=0) i na kraju (w=p, w= ‑p) funkcija faze bude jednaka nuli.

Uz zadovoljene uvjete za računanje kompleksnog logaritma prema izrazu (10.2‑8) i uz zamjenu blokova Z[ ] i Z‑1[ ] sa Fourier‑ovom odnosno inverznom Fourier‑ovom transformacijom, može se izračunati inverzna Fourier‑ova transformacija kompleksnog logaritma Fourier‑ove transformacije ulaza koja onda predstavlja izlaz karakterističnog sustava za homomorfnu dekonvoluciju, prema izrazu:

(10.2‑10)

Izlaz karakterističnog sustava, , se naziva kompleksni kepstar zbog činjenice što se u izrazu (10.2‑9) za koristi kompleksni logaritam. Pored ovog kompleksnog kepstra postoji i običan kepstar koji se uobičajeno naziva samo kepstar (engl. cepstrum). Taj pojam je u literaturi prihvaćen za označavanje inverzne Fourier-ove transformacije logaritma spektra snage signala (dakle određen je isključivo modulom frekvencijske karakteristike dok se faza ignorira). Za razliku od kompleksnog kepstra  taj običan kepstar c(n) je definiran slijedećim izrazom:

(10.2‑11)

pri čemu sekvenca c(n) predstavlja parni dio kompleksnog kepstara . Valja naglasiti da iako se koristi termin "kompleksni kepstar", da su obje sekvence  i c(n) realne sekvence, jer su određene kao inverzna Fourier-ova transformacija simetričnih spektara.

U prethodnom izlaganju definiran je karakteristični sustav za homomorfnu dekonvoluciju, kao i temeljni kanonski oblik svih sustava homomorfnih za konvoluciju. Svi sustavi ove grupe razlikuju se samo po linearnom dijelu sustava. Izbor linearnog sustava nužno ovisi o svojstvima njegovih ulaznih signala. Prema tome, pri realizaciji linearnog sustava neophodno je uzeti u obzir svojstva izlaznog signala karakterističnog sustava, tj. potrebno je proučiti svojstva kompleksnog kepstara za tipične ulazne signale, što će biti tema slijedećeg poglavlja.

1.3 Svojstva kompleksnog kepstra

Da bi se odredila svojstva kompleksnog kepstara, dovoljno je promotriti slučaj racionalne Z-transformacije. Najopćenitiji oblik razlomljene racionalne funkcije u varijabli z koji predstavlja bilo prijenosnu funkciju linearnog sustava, bilo Z-transformaciju signala x(n), može se prikazati slijedećim izrazom:

(10.3‑1)

gdje su sve vrijednosti veličina  po modulu manje od 1.

Prema tome, izrazi  i  odgovaraju nulama i polovima unutar jedinične kružnice, dok izrazi  i  odgovaraju nulama i polovima izvan jedinične kružnice. Faktor  predstavlja pomak vremenskog ishodišta, dok A predstavlja konstantu pojačanja. Uz pretpostavku da vrijedi (10.2‑8), kompleksni logaritam od X(z) je:

(10.3‑2)

Ako izraz (10.3‑2) evaluiramo na jediničnoj kružnici može se uočiti da izraz  pridonosi samo imaginarnom dijelu kompleksnog logaritma. S obzirom da ovaj izraz nosi samo informaciju o pomaku vremenskog ishodišta, može se izostaviti iz proračuna, te se stoga može zanemariti u diskusiji o svojstvima kompleksnog kepstara. Koristeći činjenicu da logaritam izraza 1-x može biti zapisan kao red potencija u varijabli x, tj.

lako je pokazati da kompleksni kepstar razlomljene racionalne funkcije X(z) ima slijedeći oblik:

(10.3‑3)

Izraz (10.3‑3) omogućava uočavanje nekoliko važnih svojstava kompleksnog kepstara. Kao prvo, kompleksni kepstar nikad nije jednak nuli, tj. neograničenog (beskonačnog) je trajanja i za pozitivne i za negativne indekse n, pa čak i kada je polazni x(n) kauzalan, stabilan i konačnog trajanja. Nadalje, očigledno je da je kompleksni kepstar padajući niz koji je po modulu ograničen s :

(10.3‑4)

gdje je  maksimum apsolutnih vrijednosti veličina , a  je konstanta proporcionalnosti.

Ako X(z) nema ni polove ni nule izvan jedinične kružnice, tj. , tada je :

(10.3‑5)

Signali (sustavi) koji zadovoljavaju navedeni uvjet se nazivaju signali (sustavi) s minimalnom fazom (engl. minimum phase). Općenito vrijedi da se nizovi oblika danog izrazom (10.3‑5) mogu u potpunosti opisati realnim dijelom svoje Fourier-ove transformacije. Stoga se kompleksni kepstar  signala s minimalnom fazom može prikazati direktno na osnovu logaritma modula Fourier-ove transformacije signala x(n), tj. na osnovu . Ovo se lako može dokazati jer vrijedi da je realni dio Fourier-ove transformacije u stvari jednak Fourier-ovoj transformaciji parnog dijela sekvence. Pošto je običan kepstar c(n) jednak parnom dijelu kompleksnog kepstra , tj. vrijedi:

 

(10.3‑6)

tada se kombiniranjem izraza (10.3‑5) i (10.3‑6) može lako pokazati da je:

(10.3‑7)

Stoga se kompleksni kepstar sekvenci s minimalnom fazom može se odrediti izračunavanjem običnog kepstra c(n) i potom primjenom izraza (10.3‑7). Sljedeći važan rezultat za sekvence s minimalnom fazom je da se kompleksni kepstar može izračunati rekurzivno iz samog ulaznog signala, a formula za to je:

(10.3‑8)

Slični rezultati se mogu dobiti u slučaju kada X(z) nema ni polove ni nule unutar jedinične kružnice. Takve signale (sustave) nazivamo signalima (sustavima) s maksimalnom fazom (engl. maximum phase). U ovom slučaju iz izraza (10.3‑3) slijedi da je

(10.3‑9)

Ukoliko upotrijebimo izraze (10.3‑6) i (10.3‑9) dolazimo do sličnog rezultata kao i u izrazima (10.3‑7) i (10.3‑8) s jedinom razlikom u tome što n < 0 i n > 0 mijenjaju mjesto.

(10.3‑10)

(10.3‑11)

Posebno interesantan slučaj je kada se ulazni signal sastoji od niz impulsa na pravilnom razmaku Np, tj. prema izrazu:

(10.3‑12)

čija je Z-transformacija dana slijedećim izrazom:

(10.3‑13)

Iz izraza (10.3‑13) evidentno je da je P(z) u stvari polinom po varijabli , a ne . Prema tome, P(z) se može izraziti kao produkt korijenih faktora oblika  i , te se lako može vidjeti da će kompleksni kepstar, , biti različit od nule samo za cjelobrojne višekratnike od . Ako radi jednostavnosti pretpostavimo da se pobudni signal sastoji od samo dva impulsa :

(10.3‑14)

tada su:

(10.3‑15)

i

(10.3‑16)

Dakle, kompleksni kepstar  je beskonačni niz impulsa razmaknutih za :

(10.3‑17)

Činjenica da je kompleksni kepstar niza jednoliko razmaknutih impulsa također jednoliko razmaknuti niz impulsa na istom razmaku, je veoma važan rezultat za analizu govora. Važno je uočiti da amplituda tih impulsa teži prema 0 kako r raste, pod uvjetom da je korijen unutar jedinične kružnice (a<1). Interesantna je i činjenica da ne postoji impuls u n=0, tj. d(n), već tek u n=Np i zatim u svim njegovim cjelobrojnim višekratnicima (r=2,3,..).