1.1 Jednolika cijev bez gubitaka

Koristan uvid u prirodu govornih signala može se dobiti razmatrajući vrlo jednostavan model u kojem se pretpostavlja da je prostorna funkcija vokalnog trakta A(x,t) konstantna i u vremenu i u prostoru (vremenski nepromjenjiva s jednolikim presjekom). Ova je konfiguracija približno točna za neutralni samoglasnik /UH/. Najprije će biti ispitan ovaj najjednostavniji model, a zatim kasnije i oni realniji i složeniji.

Slika

5.2‑1

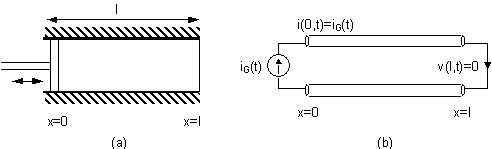
(a) Jednolika cijev bez gubitaka s idealnim zaključenjima; (b) odgovarajuća analogija s električnom linijom bez gubitaka

Slika 5.2‑1 a) prikazuje cijev jednolikog presjeka pobuđenu idealnim izvorom brzine protoka volumena zraka. Idealni izvor predstavlja klip koji se pod utjecajem vanjske sile može slobodno gibati lijevo-desno na bilo koji odabrani način i to neovisno o varijacijama tlaka u cijevi. Daljnja pretpostavka je da na otvorenom kraju cijevi nema promjene u tlaku već samo varijacije u brzini protoka volumena zraka. Ovo su očito velika zanemarenja koja je nemoguće postići u stvarnosti, međutim opravdava ih činjenica da razmatranje ovog modela kao i osnovne karakteristike rješenja dobivenih ovim postupkom imaju mnogo toga zajedničkog s puno realnijim modelima. Štoviše, pokazat će se da općenitiji modeli mogu biti sagrađeni spajanjem više ovakvih jednolikih cijevi.

Ako je funkcija A(x,t)=A konstantna, tada parcijalne diferencijalne jednadžbe (5.1‑1) i (5.1‑2) prelaze u oblik:

	(5.2‑1)
	(5.2‑2)

Može se pokazati da rješenje jednadžbi. (5.2‑1) i (5.2‑2) ima oblik:

	(5.2‑3)
	(5.2‑4)

U jednadžbama (5.2‑3) i (5.2‑4) funkcije u⁺(t-x/c) i u^-(t+x/c) mogu biti interpretirane kao valovi koji putuju u pozitivnom odnosno negativnom smjeru osi x. Međusobni odnos među tim suprotno putujućim valovima određen je rubnim uvjetima.

Iz teorije električnih linija bez gubitaka, izrazi koji povezuju napon v(x,t) i struju i(x,t) na jednolikoj (homogenoj) liniji bez gubitaka su:

	(5.2‑5)
	(5.2‑6)

gdje su L i C induktivitet, odnosno kapacitet po jedinici dužine. Može se uočiti da je teorija jednolikih električnih linija bez gubitaka direktno primjenjiva na akustičku cijev jednolikog presjeka ako usvojimo analogiju prikazanu u tablici 5.2‑1.

Tablica

5.2‑1

Analogija između akustičkih i električkih veličina

Akustička veličina	Analogna električka veličina
p – tlak	v – napon
u – brzina protoka volumena zraka	i – struja
r/A – akustički induktivitet	L – induktivitet
A/(rc^2) – akustički kapacitet	C - kapacitet

Uz ove analogije se akustička cijev jednolikog presjeka ponaša jednako kao jednolika električna linija bez gubitaka zaključena kratkim spojem (v(l,t)=0) s jedne strane, a pobuđena idealnim strujnim izvorom s druge (i(0,t)=i_G(t)). Ovo je prikazano na slici 5.2‑1 b).

Jako je korisno promotriti ponašanje linearnih sustave kao što su električne linije i krugovi u frekvencijskoj domeni. Analogno tome, mogu se napraviti slične transformacije za slučaj jednolike cijevi bez gubitaka. Prikaz ovog modela u frekvencijskoj domeni dobiva se ako se pretpostavi slijedeći rubni uvjet za x=0:

(5.2‑7)

Drugim riječima, cijev je pobuđena kompleksnom eksponencijalnom funkcijom promjene brzine protoka volumena zraka, kružne frekvencije W i kompleksne amplitude U_G(W). Pošto su jednadžbe (5.2‑1) i (5.2‑2) linearne, pretpostavljena rješenja za pozitivno i negativno putujuće valove u⁺(t-x/c) i u^-(t+x/c) također moraju biti istog oblika kao i pobuda, tj. :

	(5.2‑8)
	(5.2‑9)

Ako sada ovakva pretpostavljena rješenja uvrstimo u izraze (5.2‑3) i (5.2‑4) koji definiraju tlak i brzinu protoka duž cijevi moguće je uz poznavanje rubnih uvjeta odrediti nepoznate konstante K⁺ i K^-. Rubni uvjet na desnom kraju cijevi gdje su usne glasi:

(5.2‑10)

dok je rubni uvjet na lijevom kraju gdje su glasnice definiran izrazom (5.2‑7). Nakon određivanja konstanti K⁺ i K^- i njihovog uvrštavanja u izraze (5.2‑8) i (5.2‑9) dobiva se rješenje u stacionarnom stanju:

	(5.2‑11)
	(5.2‑12)

gdje je:

(5.2‑13)

karakteristična akustička impedancija cijevi.

Alternativni pristup koji se koristi u nastavku omogućava izbjegavanje odvojenog rješavanja za valove koji putuju u jednom odnosno drugom smjeru, tako da se rješenja za p(x,t) i u(x,t) direktno pretpostave u obliku kompleksnih eksponencijala čija kompleksna amplituda ovisi o poziciju unutar cijevi:

	(5.2‑14)
	(5.2‑15)

Uvrštenjem ovih pretpostavljenih rješenja u jednadžbe (5.1‑1) i (5.1‑2) vremenska ovisnost definirana članom e^jWt se gubi, jer se krati s lijeve i desne strane parcijalne diferencijalne jednadžbe. Radi toga dobivaju se obične diferencijalne jednadžbe koje povezuju kompleksne amplitude tlaka i brzine protoka kao funkcije pozicije x unutar cijevi.

	(5.2‑16)
	(5.2‑17)

gdje je:

(5.2‑18)

akustička impedancija po jedinici duljine, a

(5.2‑19)

akustička admitancija po jedinici duljine. Diferencijalne jednadžbe (5.2‑16) i (5.2‑17) imaju rješenje oblika:

	(5.2‑20)
	(5.2‑21)

gdje je:

(5.2‑22)

Nepoznati koeficijenti mogu se izračunati uvrštavajući rubne uvjete

	(5.2‑23)
	(5.2‑24)

Dobiveni rezultat je naravno isti kao u jednadžbama (5.2‑11) i (5.2‑12) koje izražavaju odnos između amplitude sinusoidalnog izvora brzine protoka volumena zraka na ulazu cijevi i tlaka odnosno brzine protoka volumena zraka u bilo kojoj točki u cijevi. Vrlo je interesantno promotriti odnos između brzine protoka zraka na usnama i brzine protoka na izvoru (odnos sa početka na kraj cijevi). Tako iz izraza (5.2‑12) slijedi:

(5.2‑25)

Omjer kompleksnih amplituda U(l,W) i U_G(W)

(5.2‑26)

definira frekvencijsku karakteristiku cijevi koji povezuje ulaznu i izlaznu brzinu protoka volumena zraka. Ova funkcija je nacrtana na slici 5.2‑2 a) za vrijednosti l=0.175 m i c= 350 m/s. Zamjenom W sa s/j dobivamo Laplaceovu transformaciju ili prijenosnu funkciju sustava.

(5.2‑27)

Izjednačavanjem nazivnika s nulom može se primijetiti kako V_a(s) ima beskonačan broj jednoliko razmaknutih polova na jW osi, tj. :

n=0,1,2, ...

(5.2‑28)

Slika

5.2‑2

(a) Frekvencijska karakteristika; (b) pozicije polova za jednoliku cijev bez gubitaka

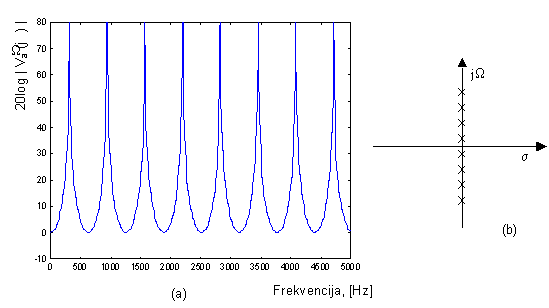
Pozicije polova su prikazane na slici 5.2‑2 b). Polovi prijenosne funkcije linearnog vremenski nepromjenjivog sustava su vlastite frekvencije sustava. Polovi također odgovaraju rezonantnim frekvencijama sustava. Kada se radi o obradi govora, rezonantne frekvencije se još nazivaju i formantne frekvencije. Slični se efekti rezonancije javljaju i kod složenijih oblika vokalnog trakta.

Treba napomenuti da poznavanje frekvencijske karakteristike sustava omogućava nalaženje odziva ne samo za sinusoidalni ulazni signal, već za bilo kakav pobudni signal uz korištenje Fourierove analize. Jednadžba (5.2‑26) se može interpretirati i kao omjer Fourierove transformacije protoka na mjestu usnica i Fourierove transformacije pobudnog signala, tj. protoka na mjestu glasnica. Zbog toga je frekvencijska karakteristika akustičkog sustava jako pogodan način njegovog opisa.