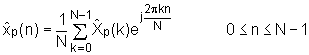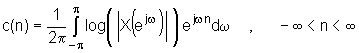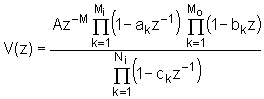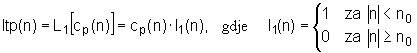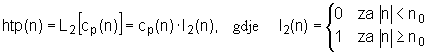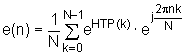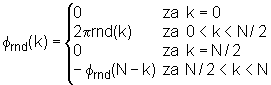1.1 Postupci izračunavanja kepstra

U prethodnom poglavlju bilo je prikazano kako se mogu formirati karakteristični sustav homomorfan za konvoluciju, kao i njegov inverz. Ako sada razmatranje ograničimo samo na ulazne signale koji imaju konačnu energiju, tada njihova z-transformacija ima područje konvergencije koje uključuje jediničnu kružnicu. To drugim riječima znači da takvi signali imaju definiranu Fourier-ovu transformaciju. U tom slučaju moguće je z-transformaciju u karakterističnom sustavu za dekonvoluciju i njegovom inverzu zamijeniti Fourier‑ovom transformacijom, kao što je već najavljeno. Za konačno duge ulazne signale, karakteristični sustav za homomorfnu dekonvoluciju opisan je slijedećim izrazima:

(10.4‑1)

(10.4‑2)

(10.4‑3)

Izrazom (10.4‑1) dana je Fourierova transformacija ulaznog signala. Izrazom (10.4‑2) dan je izraz za kompleksni logaritam Fourierove transformacije, a izrazom (10.4‑3) dana je inverzna Fourierova transformacija kompleksnog logaritma Fourierove transformacije ulaznog signala. Da bi sa ovim izrazima ((10.4‑1) do (10.4‑3)) mogli jednoznačno definirati kompleksni kepstar, potrebno je prvo definirati kompleksni logaritam Fourierove transformacije. Prvi zahtjev koji mora biti osiguran je da kompleksni kepstar realnog ulaznog signala također bude realni signal. Inverznom Fourier-ovom transformacijom dobiva se realni signal po uvjetom da je realni dio transformata bio parna funkcija, a imaginarni dio neparna funkcija od w. To znači da je za realan kompleksni kepstar potrebno osigurati da logaritam modula Fourier-ove transformacije signala bude paran po w, odnosno da faza Fourier-ove transformacije bude neparna po w. Nadalje se može pokazati da je dovoljan uvjet za jednoznačnost kompleksnog logaritma taj da faza bude kontinuirana periodička funkcija od w sa periodom 2p. Taj uvjet kontinuiteta također mora vrijediti i za  da bi bio valjana Fourierova transformacija.

Problem koji se javlja u gornjim izrazima (10.4‑1) do (10.4‑3) je potreba za izračunavanjem integrala. Taj problem se rješava aproksimacijom gornjih izraza primjenom diskretne Fourier-ove transformacije (DFT). DFT konačno dugog ulaznog signala možemo predstaviti kao otipkanu verziju Fourierove transformacije. Nadalje, DFT možemo vrlo učinkovito izračunati koristeći brzu Fourier‑ovu transformaciju (FFT).

Dakle pristup izračunavanja kompleksnog kepstra se sastoji u zamijeni Fourier‑ove transformacije DFT-om. U tom slučaju izrazi (10.4‑1) do (10.4‑3) prelaze u slijedeće:

(10.4‑4)

(10.4‑5)

(10.4‑6)

Izrazom (10.4‑6) opisan je inverzni DFT kompleksnog logaritma DFT-a ulaznog signala konačne duljine. Sufiks p upućuje da rezultirajući signali nisu potpuno jednaki onima dobivenim izrazima (10.4‑1) do (10.4‑3). To je stoga što je kompleksni logaritam  korišten u izračunavanju pomoću DFT-a otipkana verzija izraza (10.4‑2), te konačni izraz (10.4‑6) u sebi sadrži pojavu aliasing-a, odnosno preklapanja spektra. Diskretizacija spektra uzrokuje periodičnost kepstra, tj. kompleksni kepstar izračunat pomoću DFT-a možemo dobiti periodičkim ponavljanjem kompleksnog kepstra izračunatog korištenjem prave Fourierove transformacije svakih N uzoraka, tj. prema slijedećem izrazu:

(10.4‑7)

Blok shema karakterističnog sustava za dekonvoluciju za izračunavanje kompleksnog kepstra primjenom DFT-a prikazana je na slici 10.4‑1.

Slika

10.4‑1

Postupak izračunavanja kompleksnog kepstra

Kod kompleksnog kepstra koristi se kompleksni logaritam. Međutim kod običnog kepstra računa se samo običan logaritam modula Fourier-ove transformacije, kao što je dano izrazom (10.4‑8).

(10.4‑8)

I u ovom slučaju može se koristiti aproksimacija stvarnog kepstra korištenjem DFT-a umjesto Fourier-ove transformacije. To znači da se kepstar cp(n) nalazi kao inverzni DFT logaritma modula DFT-a ulaznog niza, tj. prema izrazu:

(10.4‑9)

I u ovom slučaju zbog pojave aliasinga uslijed otipkavanja Fourier-ove transformacije aproksimacija kepstra cp(n) i stvarni kepstar su vezani slijedećim izrazom:

(10.4‑10)

Na slici 10.4‑2 prikazana je blok shema postupka određivanja kepstra cp(n).

 

Slika

10.4‑2

Postupak izračunavanja kepstra korištenjem DFT-a

Zbog opisane pojave aliasinga kod korištenja DFT-a, potrebno je računanje DFT-a provesti sa velikim brojem uzoraka N. Velika rezolucija otipkavanja Fourier-ove transformacije potrebna je i kod izračunavanja kompleksnog logaritma, gdje je potrebno osigurati kontinuitet fazne karakteristike. Korištenje velikog broja uzorka (N=512 ili više) ne predstavlja problem pošto je diskretnu Fourier-ovu transformaciju moguće realizirati pomoću brzih algoritama kao što je FFT.

1.1.1 Kepstar i kompleksni kepstar govornog signala

Postupci vremenski kratkotrajne analize govornog signala, kod kojih se analiza provodi nad segmentima konačnog trajanja, lako se mogu primijeniti i na homomorfnu obradu. Model formiranja govornog signala temeljen je na vremenski sporo promjenjivom linearnom sustavu pobuđenim s periodičnim nizom impulsa ili sa slučajnim šumom. Za dovoljno kratki segment govora može se pretpostaviti sa su parametri sustava bili stalni. Stoga za kratki zvučni segment govora moguće je pretpostaviti da je nastao pobuđivanjem linearnog vremenski nepromjenjivog sustava periodičnim nizom impulsa p(n) perioda Np.

(10.4‑11)

Segment govora s(n) dobiva se periodičkim ponavljanjem impulsnog odziva hv(n) svakih Np uzoraka. Impulsni odziv linearnog sustava hv(n) obuhvaća valni oblik glotalnog pulsa g(n), impulsni odziv vokalnog trakta v(n) i impulsni odziv zračenja na usnicama r(n).

Analogno tome, kratki segment bezvučnog govora se dobiva pobuđivanjem linearnog sustava s impulsnim odzivom hu(n) sa slučajnim šumom u(n).

(10.4‑12)

U ovom slučaju impulsni odziv linearnog sustava hu(n) obuhvaća impulsni odziv vokalnog trakta i impulsni odziv zračenja na usnicama. Izraze (10.4‑11) i (10.4‑12) moguće je zapisati i u z-domeni:

(10.4‑13)

Za analitičko izračunavanje kompleksnog kepstara govornog signala, potrebno je poznavati ove tri prijenosne funkcije G(z), V(z) i R(z). Prijenosna funkcija vokalnog trakta V(z) ima slijedeći opći oblik:

(10.4‑14)

Za sve zvučne glasove osim nazalnih, V(z) ima samo polove, tj. ak=0 i bk=0 za sve k. Kod nazalnih glasova i kod bezvučnih glasova prijenosna funkcija sadrži i polove i nule. Neke od tih nula se mogu nalaziti i izvan jedinične kružnice, ali zbog razloga stabilnosti svi polovi ck moraju biti unutar kružnice. Pošto je impulsni odziv v(n) realan, polovi i nule se ili pojavljuju u konjugirano kompleksnim parovima, ili su realni.

Efekt zračenja na usnicama moguće je u grubo modelirati visoko propusnom funkcijom oblika:

(10.4‑15)

Kod zvučnih glasova ukupna prijenosna funkcija ovisi i o z-transformaciji valnog oblika glotalnog pulsa g(n), koji je vremenski niz konačnog trajanja pa se stoga i može modelirati kao FIR sustav:

(10.4‑16)

gdje su ak i bk nule koje se nalaze unutar odnosno izvan jedinične kružnice.

Uz ovako zadane prijenosne funkcije i uz poznavanje svojstava kompleksnog kepstra koja su diskutirana u poglavlju 10.3, moguće je predvidjeti očekivani oblik kompleksnog kepstra. Za zvučne glasove, ukupna prijenosna funkcija Hv(z) imat će polove unutar jedinične kružnice i nule unutar i izvan jedinične kružnice, pa se stoga može zaključiti da se ne radi o funkciji minimalne faze. Zbog tog razloga kompleksni kepstar će biti različit od nule i lijevo i desno od n=0. Pošto se kod zvučnih glasova pobuda može predstaviti periodičnim nizom jediničnih impulsa na razmaku Np, može se očekivati da se u kompleksnom kepstru zvučnog segmenta pojave šiljci na indeksu Np i njegovim cjelobrojnim višekratnicima. Slična svojstva vrijede i za običan kepstar c(n), koji predstavlja parni dio kompleksnog kepstra , i koji će upravo zbog tog svojstva parnosti biti simetričan oko nule.

Ova svojstva će biti ilustrirana na primjeru kepstra cp(n) govornog odsječka glasa 'e' otipkanog s frekvencijom otipkavanja fs=8000 Hz. prikazanog na slici 10.4‑3. Kepstralna analiza je provedena korištenjem DFT-a u N=256 točaka, prema blok shemi prikazanoj na slici 10.4‑2.

Slika

10.4‑3

Valni oblik govornog signala za samoglasnik 'e'

Prije izračunavanja DFT-a potrebno je signal pomnožiti s vremenskim otvorom. Kod obrade govornih signala vrlo se često koristi Hamming-ov vremenski otvor, no moguće je koristiti i druge vremenske otvore s dobrim spektralnim svojstvima. U slučaju korištenja pravokutnog vremenskog otvora, dolazi do pojave spektralnog rasipanja, gdje spektralne komponente velikih amplituda prekrivaju svojim bočnim laticama spektralne komponente malih amplituda. Ovime se potpuno gubi formantna struktura, jer DFT vrlo loše aproksimira stvarni spektar, zbog konvolucije sa sporo padajućim spektrom pravokutnog vremenskog otvora. Signal sa slike 10.4‑3 nakon množenja s Blackman-ovim vremenskim otvorom prikazan je na slici 10.4‑4.

Slika

10.4‑4

Signal pomnožen s Blackman-ovim vremenskim otvorom

 

Slika

10.4‑5

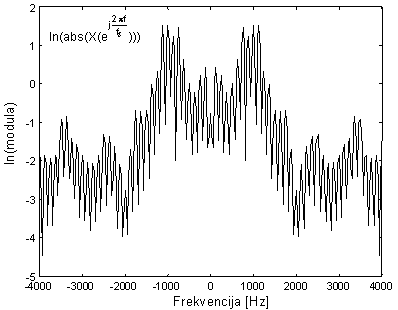
Prirodni logaritam modula DFT-a

Prirodni logaritam modula diskretne Fourier-ove transformacije signala sa slike 10.4‑4 prikazan je na slici 10.4‑5. Pojava periodičnih latica na slici 10.4‑5 je posljedica periodičnosti pobudnog signala vokalnog trakta. DFT idealnog pobudnog signala vokalnog trakta p(n) jednak je ovome prikazanom na slici 10.4‑5, s tom razlikom da su sve latice iste visine. Amplitude latica prikazanih na slici 10.4‑5 određene su prijenosnom funkcijom Hv(z) za , tj. otipkanom prijenosnom funkcijom u N ekvidistantnih točaka na jediničnoj kružnici. Zbog toga moguće je zaključiti da je sporo promjenljiva spektralna ovojnica određena prijenosnom funkcijom Hv(z), dok su brze oscilacije određene DFT-om pobudnog signala p(n). Razmak između svake dvije susjedne latice odgovara osnovnoj frekvenciji titranja glasnica. U primjeru na slici 10.4‑5 moguće je prebrojiti 32 latice na intervalu od 0 do 4000 Hz, pa se lako može procijeniti da osnovna frekvencija iznosi f0=125 Hz. Nakon logaritmiranja modula DFT-a ova dva dijela (ovojnica i brzo oscilirajuće latice) vezana su aditivnom superpozicijom. Ako za kratko ignoriramo činjenicu da slika 10.4‑5 prikazuje modul spektra signala prikazan u logaritamskom mjerilu, nego ga interpretiramo kao običan vremenski promjenljiv valni oblik, tada u tom valnom obliku lako prepoznajemo dva dijela: prvi sporo promjenljivi dio i drugi brzo oscilirajući dio. Drugim riječima, nisko odnosno visoko propusnom filtracijom ovog signala bilo bi moguće razdvojiti ta dva dijela. Isto tako ako bi izračunali Fourier-ovu transformaciju tog signala, sporo promjenljive komponente nalazile bi se na frekvencijama blizu nule, dok bi se brzo promjenljiva komponenta pojavila kao šiljci na mjestima koja odgovaraju cjelobrojnim višekratnicima frekvencije tih brzih oscilacija. Ovo je i bila originalna zamisao autora koji je prvi predložio postupke dekonvolucije temeljene na logaritmu modula DFT-a. Pojam kepstra upravo proizlazi iz činjenice da se ovdje radi o svojevrsnom spektru od spektra, pa je autor predložio naziv kepstar koji se formira od riječi spektar tako da se izvrne redoslijed prva četiri slova. Kasnije je ovaj inženjerski pristup upotpunjen matematičkim modelom homomorfne obrade koji se temelji na z-transformaciji i kompleksnom kepstru, koji je opisan u prošlom poglavlju. Iako se u karakterističnom sustavu za dekonvoluciju nakon logaritmiranja koristi inverzna diskretna Fourier-ova transformacija (izrazi (10.4‑6) odnosno (10.4‑9)), a ne diskretna Fourier-ova transformacija kao što je to bilo originalno predloženo, gore opisana svojstva za slučaj Fourier-ove transformacije logaritma modula DFT-a signala biti će identična. DFT i inverzni DFT se razlikuju isključivo u faktoru skale (1 za DFT, odnosno 1/N za inverzni) i u fazama baznih funkcija transformacije ( za DFT, odnosno  za inverzni). Kepstar cp(n) dobiven inverznom DFT transformacijom prirodnog logaritma modula DFT-a signala sa slike 10.4‑4 prikazan je na slici 10.4‑6.

Slika

10.4‑6

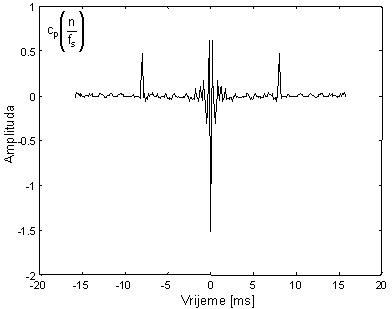
Kepstar glasa 'e'

Brzo padajući dio kepstra oko nule (približno ±3ms) proizlazi od sporo promjenljive spektralne ovojnice DFT-a, tj. jednoznačno opisuje modul prijenosne funkcije Hv(z), koja je određena valnim oblikom glotalnog pulsa, impulsnim odzivom vokalnog trakta i utjecajem zračenja na usnicama. S druge strane, pulsevi na pozicijama –8ms i +8ms su posljedica periodičnosti pobudnog signala vokalnog trakta osnovne frekvencije f0=125 Hz. Vrlo značajno svojstvo koje je vidljivo na slici 10.4‑6 jest činjenica da su te dvije komponente kepstra razdvojene u vremenu, tj. dio blizak nuli (engl. low time part) je određen sa hv(n), dok je preostali dio koji je daleko od nule (engl. high time part) određen sa p(n). Vremenska dislokacija ta dva aditivno vezana dijela će omogućiti njihovo razdvajanje običnim (jednostavnim) linearnim sustavom (vremenskim otvorom).

U slučaju korištenja kompleksnog kepstra, potrebno je izračunati i fazu DFT-a. Za signal sa slike 10.4‑4, osnova vrijednost faze (-p do p) prikazana je na slici 10.4‑7.

Slika

10.4‑7

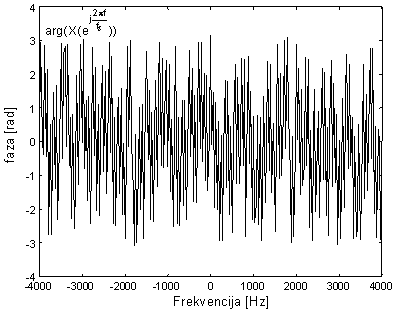
Faza DFT-a segmenta govornog signala glasa "e"

 

Kao što je već opisano potrebno je osigurati kontinuiranost ove fazne karakteristike, tj. na svim mjestima gdje je fazni skok sumjerljiv sa 2p, potrebno je fazi prikazanoj na slici 10.4‑7 pribrojiti cjelobrojni višekratnik od 2p. Ovaj postupak nije jednostavan, jer linearni fazni član uslijed vremenskog pomaka glotalnog pulsa u odnosu na poziciju vremenskog otvora može imati vrlo veliki nagib, pa je vrlo teško odrediti pozicije stvarnih 'preskoka'. Stvar se dodatno komplicira kod zvučnih glasova gdje uslijed periodičnosti pobudnog signala velik broj komponenata DFT-a može imati modul blizak nuli. Faza tih komponenata određena je šumom i numeričkim pogreškama, a ne fazom pobudnog signala p(n) i fazom prijenosne funkcije Hv(z). To su razlozi zbog kojih se kompleksni kepstar rijetko koristi, pa se većina postupaka numeričke homomorfne analize govornog signala ograničava na običan kepstar cp(n) prikazan na slici 10.4‑6.

 

Slika

10.4‑8

Blok shema sustava za homomorfnu dekonvoluciju govora korištenjem DFT-a

Korištenjem opisanog svojstva razdvajanja pobudnog signala i prijenosne funkcije linearnog sustava u kepstralnoj domeni moguće je formirati cijeli sustav za homomorfnu dekonvoluciju. Blok shema takvog sustava prikazana je na slici 10.4‑8. Govorni signal s(n) množi se s vremenskim otvorom w(n), te se na tako izdvojenom segmentu govornog signala primjenjuje karakteristični sustav za homomorfnu dekonvoluciju D*[ ], čiji je izlaz kepstar cp(n). Na kepstar se primjenjuju dva linearna operatora L1[ ] i L2[ ], te se ta dva dijela zatim propuštaju kroz inverzni karakteristični sustav D*-1[ ]. Ovaj postupak rezultira s dva izlazna signala h(n) i e(n). Uz pravilno odabrane linearne operatore L1[ ] i L2[ ], h(n) će biti jednak impulsnom odzivu linearnog sustava, dok će e(n) biti jednak njegovoj pobudi. Iz diskusija o svojstvima kepstra cp(n) prikazanog na slici 10.4‑6, lako se može zaključiti da se operator L1[ ], koji treba primijeniti na cp(n) radi izdvajanja impulsnog odziva sustava, može realizirati običnim kepstralnim vremenskim otvorom l1(n), prema izrazu (10.4‑17).

(10.4‑17)

Opisanim postupkom se izdvaja n0-1 uzoraka kepstra lijevo i desno od nule. Ovaj dio kepstra se naziva 'low time part' ili ltp dio, jer odgovara dijelu s 'niskim' vremenskim indeksima. Rubni indeks n0 se odabire tako da ne zahvati pulseve uslijed periodičnosti pobude, tj. n0<fs/f0, gdje je fs frekvencija otipkavanja, a f0 osnovna frekvencija titranja glasnica. Operator L2[ ], je komplementaran operatoru L1[ ], tj. on propušta ono što L1[ ] ne propušta, pa vrijedi izraz:

(10.4‑18)

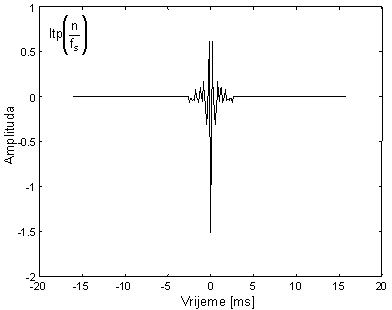
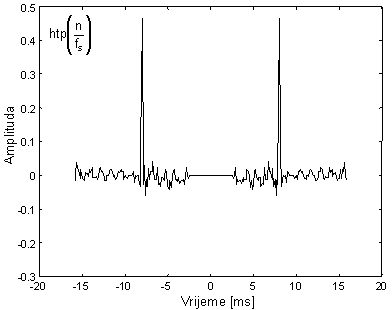
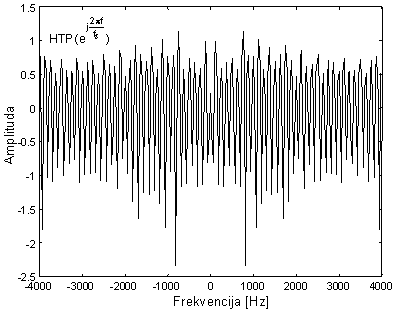
Izlaz ovog operatora se naziva 'high time part' ili htp dio kepstra jer odgovara 'visokim' vremenskim indeksima. Na slikama 10.4‑9 i 10.4‑10 prikazani su ltp i htp dio kepstra sa slike 10.4‑6, uz rubni indeks n0=20, što odgovara intervalu ±2.5 ms oko nule.

Slika

10.4‑9

Nisko-vremenski dio kepstra (ltp)

Slika

10.4‑10

Visoko-vremenski dio kepstra (htp)

Ova dva dijela se zatim obrađuju inverznim karakterističnim sustavom D*-1[ ], a prvi korak u toj obradi je izračunavanje DFT-a ta dva signala. Pošto su oba signala parna (simetrična oko nule) DFT će biti realni (imaginarni dijelovi su jednaki nula). DFT od ltp dijela i DFT od htp dijela kepstra prikazani su na slikama 10.4‑11 i 10.4‑12.

Slika

10.4‑11

DFT ltp dijela kepstra

Na ovim slikama je vidljiv rezultat željene operacije razdvajanja dvije konvolvirane komponente (pobudnog signala i impulsnog odziva sustava) na sumu dvije DFT transformacije. Pošto je suma operatora L1[ ] i L2[ ] jednaka jediničnom operatoru, suma DFT-a od ltp dijela i DFT-a od htp dijela kepstra je identički jednaka logaritmu modula DFT‑a koji je prikazan na slici 10.4‑5.

Slika

10.4‑12

DFT htp dijela kepstra

Radi bolje ilustracije činjenice da ltp dio kepstra jednoznačno opisuje sporo promjenljivu spektralnu ovojnicu govornog signala, na slici 10.4‑13 prikazan je prirodni logaritam modula DFT-a signala sa slike 10.4‑4, zajedno s DFT-om ltp dijela kepstra. Radi jasnijeg prikaza DFT ltp dijela je podignut u odnosu na pravu poziciju za 2 prema gore.

Slika

10.4‑13

Modeliranje spektralne ovojnice ltp dijelom kepstra

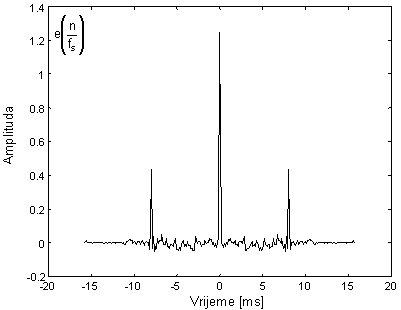
Završni korak u ovom postupku homomorfne dekonvolucije je eksponenciranje ovih DFT-a, i izračunavanje inverzne DFT transformacije, što rezultira signalima h(n) i e(n). Ovi signali su također parni, jer kod korištenja običnog kepstra (za razliku od kompleksnog kepstra), DFT od ltp i htp dijela kepstra su realni. Pobudni signal e(n) je vrlo sličan idealnom pobudnom signalu za zvučne glasove (niz jediničnih impulsa), s time da amplituda ovih pulseva opada u skladu s oblikom primijenjenog vremenskog otvora w(n).

Slika

10.4‑14

Impulsni odziv linearnog sustava, h(n)

Slika

10.4‑15

Pobudni signal linearnog sustava e(n)

Konvolucijom ova dva signala e(n) i h(n) trebao bi se dobiti početni govorni segment x(n) izdvojen vremenskim otvorom. Međutim, ovo vrijedi samo u slučaju korištenja kompleksnog kepstra . U slučaju korištenja običnog kepstra cp(n), dobiva se signal prikazan u gornjoj polovici slike 10.4‑16 koji se očito razlikuje od signala x(n) prikazanog u donjoj polovici iste slike. Ako bi se izračunao DFT od ova dva signala u istom broju točaka N koji je korišten i kod kepstralne analize, pokazalo bi se da su moduli ta dva DFT-a identički jednaki, tj. da se ta dva signala razlikuju isključivo po fazi. Ovakav rezultat se i mogao očekivati obzirom da je kepstar cp(n) izračunat isključivo na osnovu modula DFT-a signala x(n), dok je faza ignorirana.

Slika

10.4‑16

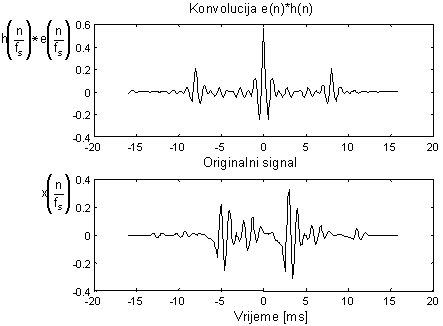
Konvolucija signala e(n) i h(n) i početni signal x(n)

Svi opisani postupci se mogu primijeniti i na bezvučni govorni segment. U slijedećem primjeru koristit će se glas 'š', kao primjer bezvučnog frikativa. Parametri kepstralne analize identični su onima za glas 'e', tj. fs=8000Hz, N=256 i Blackman-ov vremenski otvor. Izdvojeni govorni segment pomnožen s vremenskim otvorom prikazan je na slici 10.4‑17.

Slika

10.4‑17

Bezvučni segment pomnožen s Blackman-ovim vremenskim otvorom

Slika

10.4‑18

Prirodni logaritam modula DFT-a

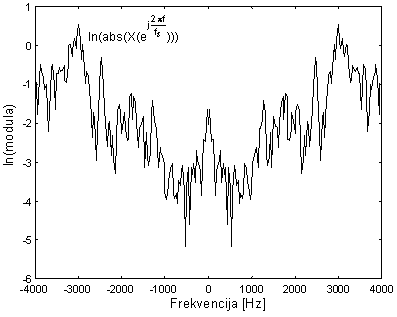
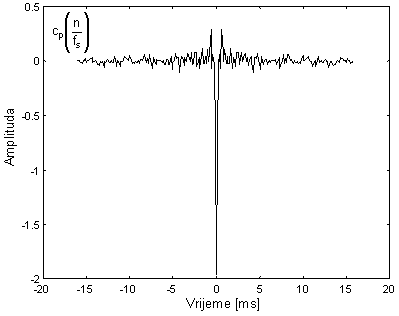
Prirodni logaritam modula diskretne Fourier-ove transformacije signala x(n) sa slike 10.4‑17, prikazan je na slici 10.4‑18. U ovom spektru je vidljiva formantna struktura, s značajnim formantom na frekvenciji 3000 Hz, i par slabijih formanata na nižim frekvencijama. Za razliku od zvučnog segmenta kod kojeg je 'fina' spektralna struktura bila pravilna i periodična, kod bezvučnog glasa 'š', brze oscilacije su nepravilne (šumovite) i aperiodske. Zbog te činjenice u kepstru cp(n) prikazanom na slici 10.4‑19 više ne postoje izraženi maksimumi osim onog za n=0. Taj nulti kepstralni koeficijent cp(0) nosi informaciju o energiji ulaznog signala, i nalazi se kao integral prirodnog logaritma modula spektra normiran sa 2p.

Slika

10.4‑19

Kepstar bezvučnog glasa 'š'

Slika

10.4‑20

Nisko-vremenski dio kepstra (ltp) glasa "š"

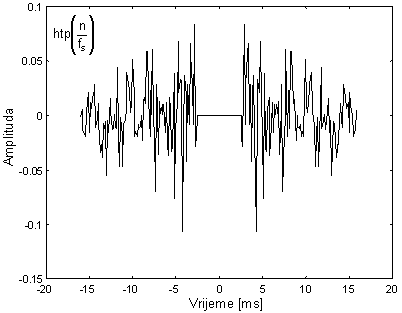
Nakon razdvajanja na nisko-vremenski i visoko-vremenski dio operatorima L1[ ] i L2[ ] uz n0=20, dobivaju se ltp(n) i htp(n) prikazani na slikama 10.4‑20 i 10.4‑21. Nisko‑vremenski dio pokazuje brzo padajući karakter jednako kao i kod zvučnih glasova, dok se visoko-vremenski dio potpuno razlikuje, tj. pokazuje šumovit karakter bez ikakvih izraženih maksimuma.

Slika

10.4‑21

Visoko-vremenski dio kepstra (htp) glasa "š"

Slika

10.4‑22

Modeliranje spektralne ovojnice ltp dijelom kepstra

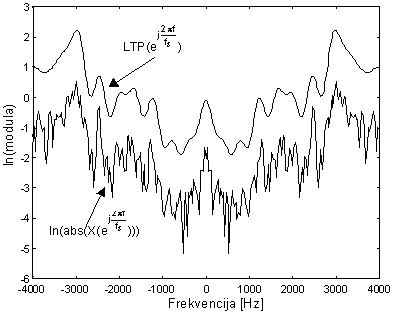
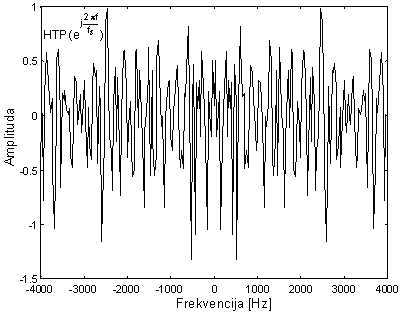
Primjenom diskretne Fourier-ove transformacije na ltp(n) dobiva se spektralna ovojnica signala koja je prikazana na slici 10.4‑22 zajedno s prirodnim logaritmom modula DFT-a signala x(n) pomnoženog s vremenskim otvorom. Iz ovog primjera je vidljivo da ltp dio kepstra i kod bezvučnih glasova dobro modelira spektralnu ovojnicu, tj. formantnu strukturu govornog signala. DFT visoko-vremenskog dijela htp(n), prikazan je na slici 10.4‑23 i ima oblik spektra bijelog šuma. To znači da su sve spektralne komponente sličnih amplituda, ali ne postoji nikakva pravilnost ili periodičnost. Potrebno je ponovno naglasiti, da u slučaju korištenja običnog kepstra cp(n), koji je paran, sve komponente DFT-a htp i ltp dijela imaju nultu-fazu, tj. realne su. Ova činjenica imat će utjecaja na oblik pobudnog signala e(n), koji se nalazi na osnovu spektra prikazanog na slici 10.4‑23.

Slika

10.4‑23

DFT htp dijela kepstra

Slika

10.4‑24

Impulsni odziv linearnog sustava, h(n)

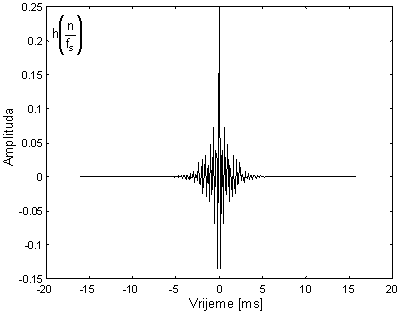
U skladu s blok shemom obrade na slici 10.4‑8, eksponenciranjem i inverznom diskretnom Fourier-ovom transformacijom DFT-a od ltp i htp dijela kepstra dobivaju se impulsni odziv linearnog sustava h(n) prikazan na slici 10.4‑24 i pobudni signal sustava e(n) prikazan na slici 10.4‑25. Impulsni odziv sustava h(n) odgovara očekivanjima i u slučaju bezvučnog glasa obuhvaća samo impulsni odziv vokalnog trakta i impulsni odziv zračenja na usnicama. U njemu su vidljiva visoko-frekvencijska istitravanja vlastitim frekvencijama sustava, od kojih je najizraženija frekvencija na mjestu najznačajnijeg formanta (3000Hz). S druge strane, pobudni signal sustava e(n) ne odgovara početnim pretpostavkama, tj. kod bezvučnih glasova korištena je pretpostavka da je pobudni signal sustava u(n) u izrazu (10.4‑12) slučajni šum, a ne jedinični impuls kao što je prikazano na slici 10.4‑25. Do ove pojave dolazi zbog toga što sve komponente DFT-a htp dijela imaju nultu-fazu, pa se idealno pribrajaju na vremenskom indeksu n=0 (koherentne su).

Slika

10.4‑25

Pobudni signal linearnog sustava e(n)

Slika

10.4‑26

Pobudni signal sa slučajnom fazom ernd(n)

Ovaj problem moguće je riješiti promjenom fazne karakteristike pobudnog signala. Kao što je već napomenuto kod primjera zvučnog glasa, u slučaju korištenja običnog kepstra konvolucija e(n)*h(n) nije identički jednaka signalu x(n), već su ta dva signala jednaka isključivo po modulu DFT-a. To drugim riječima znači da se faza svakog od ta tri signala, e(n), h(n) i x(n), može po želji mijenjati, a da i dalje vrijedi jednakost modula DFT-a. U skladu s ovim pravilom, može se provesti modifikacija faze DFT-a htp dijela, koja bi rezultirala s pobudnim signalom koji je sličniji bijelom šumu.

(10.4‑19)

(10.4‑20)

(10.4‑21)

(10.4‑22)

Izrazi (10.4‑19) i (10.4‑20) opisuju postupak izračunavanja pobude e(n) prikazane na slici 10.4‑25. U izrazu (10.4‑21) vidljiv je postupak modifikacije faze, tj. svakoj eksponenciranoj komponenti HTP(k) dodaje se slučajni fazni pomak frnd(k), koji će razbiti sinfaznost na nultom uzorku (n=0). Pošto izlazni signal ernd(n) mora biti realan, potrebno je osigurati antisimetričnost faze oko w=0, kao što se to vidi iz izraza (10.4‑22). Slučajna faza frnd(k) se izračunava na osnovu niza od N/2-1 slučajnih brojeva rnd(k) na intervalu [0,1], s jednolikom razdiobom.

Slika

10.4‑27

Konvolucija signala ernd(n) i h(n) i početni signal x(n)

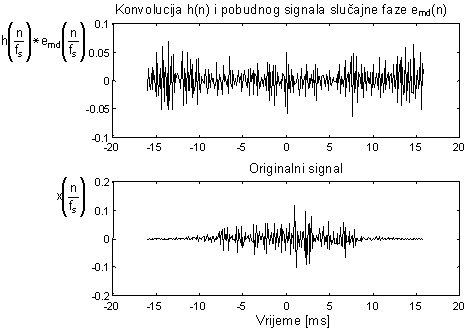
Ovakav postupak modifikacije fazne karakteristike rezultira pobudnim signalom ernd(n) prikazanim na slici 10.4‑26, čiji je modul DFT-a identički jednak modulu DFT-a signala e(n). Drugim riječima, iako se valni oblici ta dva signala značajno razlikuju, razlika je sadržana isključivo u faznom članu.

Na gornjoj polovici slike 10.4‑27 prikazan je signal koji se dobiva konvolucijom modificiranog pobudnog signala ernd(n) i impulsnog odziva sustava h(n). Ovaj se signal po valnom obliku razlikuje od početnog signala x(n) koji je prikazan u donjoj polovici iste slike, ali moduli DFT transformacija u N točaka ova dva signala su identički jednaki. Korištenje kompleksnog kepstra u svrhu očuvanja faznih odnosa kod zvučnih glasova može imati opravdanje, međutim kod bezvučnih glasova fazna karakteristika s perceptualnog stanovišta ne igra nikakvu ulogu. To znači da faza bezvučnog glasa može biti proizvoljno podešena, a da se taj glas i dalje čuje kao isti glas.

Teoretska analiza i primjeri dani u ovom poglavlju pokazali su da je primjenom homomorfne dekonvolucije govornog signala moguće odrediti aproksimacije pojedinih komponenti konvolucije, tj. rastaviti govorni signal na pobudu i impulsni odziv linearnog sustava. Međutim, kod većine primjena homomorfne obrade govora, ne traži se cjelokupni postupak dekonvolucije. Na primjer, u slučaju određivanja osnovne frekvencije titranja glasnica ili određivanja frekvencija formanata, dovoljno je provesti prvi dio postupka, tj. određivanje kepstra. Primjeri kepstra zvučnog i bezvučnog glasa prikazani na slikama 10.4‑6 i 10.4‑19 sugeriraju mogućnost određivanja informacije o zvučnosti govornog segmenta isključivo na osnovnu kepstra. Također na osnovu pozicije izraženih maksimuma u kepstru zvučnih glasova moguće je direktno odrediti frekvenciju titranja glasnica. Pošto ltp dio kepstra jednoznačno opisuje spektralnu ovojnicu izdvojenog govornog segmenta, tj. njegovu formantnu strukturu, moguće je odrediti frekvencije formanata postupcima traženja pozicija lokalnih maksimuma u DFT-u ltp dijela. U slijedećem poglavlju biti će opisani postupci određivanja osnovne frekvencije titranja glasnica korištenjem kepstra.