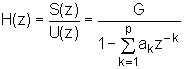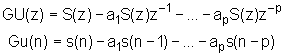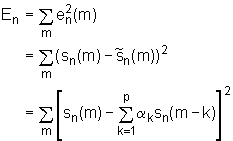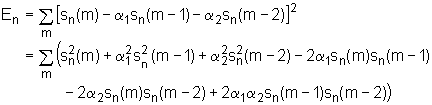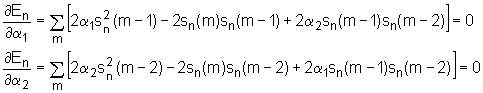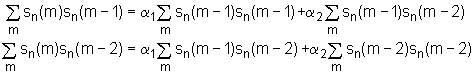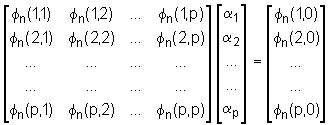1. Postupci linearne predikcije govornih signala

1.1 Uvod u linearnu predikciju

Metoda linearne predikcije je jedna od najdjelotvornijih metoda analize govora. Ova metoda je postala prevladavajuća tehnika određivanja (estimacije) osnovnih parametara govora, npr.: osnovne frekvencije titranja glasnica, formanata, kratkotrajnih spektralnih svojstava, funkcije površine poprečnog presjeka vokalnog trakta, te za predstavljanje govora kod prijenosa ili pohrane korištenjem malog broja bita. Važnost ove metode je u mogućnosti pronalaženja izuzetno točnih estimacija parametara, te u relativno velikoj brzini izračunavanja, tj. maloj numeričkoj složenosti postupka. U ovom poglavlju bit će predstavljena formulacija osnovne ideje metode linearne predikcije, te diskusija o važnijim aspektima korištenja ove metode u stvarnim aplikacijama za obradu govora.

Osnovna ideja metode linearne predikcije je u pretpostavci da se uzorak signala može aproksimirati linearnom kombinacijom prethodnih uzoraka. Unikatni skup "najboljih" koeficijenata prediktora može se odrediti minimizacijom sume kvadrata razlike stvarnih uzoraka govora i uzoraka dobivenih linearnom predikcijom na ograničenom vremenskom intervalu. (Koeficijenti prediktora su težinski koeficijenti koji se koriste u linearnoj kombinaciji prethodnih uzoraka.)

Teoretska osnova postupka linearne predikcije je blisko povezana s osnovnim govornim modelom koji je opisan u prethodnim poglavljima, gdje je pokazano da govor može biti modeliran kao izlaz iz linearnog, vremenski promjenjivog sustava pobuđenog kvazi-periodičnim nizom impulsa (za vrijeme zvučnog govora), ili slučajnim šumom (za vrijeme bezvučnog govora). Metoda linearne predikcije omogućuje robustnu, pouzdanu i točnu metodu određivanja parametara koji karakteriziraju takav linearni, vremenski promjenjivi sustav.

U ovom poglavlju dan je općeniti pregled analize linearnom predikcijom, i bit će pokazano kako osnovna ideja linearne predikcije vodi ka skupini od nekoliko tehnika analize koje se mogu koristiti za određivanje parametara govornog modela. Ovaj općeniti skup tehnika analize linearnom predikcijom se često naziva kodiranje linearnom predikcijom (engl. Linear Predictive Coding, LPC).

Tehnike i metode linearne predikcije su već dugo poznate u inženjerskoj literaturi. Tako npr. linearna predikcija se koristi u području automatske regulacije i upravljanja gdje je poznata pod nazivom "estimacija sustava", ili pak u području teorije informacija gdje se naziva "identifikacija sustava". Ovaj zadnji naziv je posebno ilustrativan, jer ukazuje na činjenicu da je korištenjem LPC postupaka moguće odrediti koeficijente prediktora, koji jednoznačno opisuju (identificiraju) nepoznat sustav na osnovu njegovog izlaza, te ga modeliraju digitalnim rekurzivnim filtrom bez nula.

Sa stanovišta primjene u obradi govora, pojam linearne predikcije se odnosi na niz praktično ekvivalentnih formulacija problema modeliranja govornog signala. Razlike između ovih formulacija su prvenstveno u načinu gledanja na problem, a u nekim slučajevima razlike se odnose i na detalje proračuna kojim se određuju parametri prediktora. Konkretno, značajnije formulacije analize linearnom predikcijom primijenjene u obradi govora su:

1. metoda kovarijance (engl. the covariance method)

2. metoda autokorelacije (engl. the autocorrelation formulation)

3. metoda korištenjem mrežaste strukture (engl. the lattice method)

4. metoda inverznog filtra (engl. the inverse filter formulation)

5. metoda određivanja spektra (engl. the spectral estimation formulation)

6. metoda maksimalne sličnosti (engl. the maximum likelihood formulation)

7. metoda unutrašnjeg produkta (engl. inner product formulation)

U nastavku će biti detaljno razmotrene samo prve tri metode s obzirom da su ostale u biti jednake jednoj od te prve tri. Postupak linearne predikcije je vrlo važan u području obrade govornog signala, prvenstveno zbog činjenice što se osnovni model linearne predikcije vrlo dobro poklapa s modelima formiranja govornog signala diskutiranim u prethodnim poglavljima. Najveće težište ovog poglavlja biti će na diskusiji kako je moguće pouzdano odrediti parametre govornog modela primjenom postupka linearne predikcije, a biti će najavljene i moguće primjene ovog postupka u obradi govora.

1.2 Primjer predikcije govornog signala

Interesantno je proučiti učinkovitost postupka linearne predikcije govornog signala i prije njegove formalne definicije. Na slici 9.2‑1 a) prikazan je kratki odsječak valnog oblika govornog signala s(n), za glas 'u' otipkan s frekvencijom f_s=8kHz. Slikom 9.2‑1 ilustrirano je kako se postupkom linearne predikcije izračunava predikcija uzorka s(5) na osnovu p=10 uzoraka koji mu prethode, tj. na osnovu s(4), s(3), ... s(-4), s(5). Točnije rečeno predikcija uzorka s(n), označena sa se izračunava kao linearna kombinacija uzoraka s(n‑1), s(n‑2), ... s(n‑p), gdje je p stupanj (ili red) prediktora. Koeficijenti te linearne kombinacije neka su označeni sa a₁ do a_p, pa se predikcija nalazi kao:

(9.2‑1)

Koeficijenti prediktora su prikazani na slici 9.2‑1 b) u vremenskom položaju za predikciju n=5-tog uzorka. Za prvu ruku pretpostavimo da su ti koeficijenti unaprijed poznati i da su zadani tablicom 9.2‑1.

Tablica

9.2‑1

Koeficijenti linearnog prediktora za glas 'u'

a10	a9	a8	a7	a6	a5	a4	a3	a2	a1
-0.312	0.550	-0.664	0.585	-0.212	0.128	-0.779	0.866	-0.865	1.363

Predikcija za uzorke n=0 do 9, izračunata primjenom skupa koeficijenata iz tablice 9.2‑1, prikazana je na slici 9.2‑1 c) i uistinu pokazuje sličnost s originalnim signalom s(n) prikazanim na 9.2‑1 a). Razlika između stvarne vrijednosti n-tog uzorka i njegove predikcije e(n)=s(n)‑ se naziva predikcijskom pogreškom, a prikazana je na slici 9.2‑1 d). Na primjer, uzorak signala na indeksu n=5 iznosi s(5)=, predviđeni uzorak iznosi =, a predikcijska pogreška iznosi e(5)=.

Koeficijenti prediktora su isti (stalni) za predikciju svih uzoraka unutar nekog promatranog intervala, a cilj 'dobre' predikcije je odabrati koeficijente prediktora tako da pogreška predikcije svih uzoraka bude što je moguće manja. Kod klasičnih postupaka linearne predikcije, kao mjera kvalitete predikcije koristi se suma kvadrata predikcijske pogreške na tom promatranom intervalu. Promatrani interval redovito je višestruko duži od reda prediktora, pa stoga odabir prediktora po kriteriju najmanje kvadratne predikcijske pogreške predstavlja određeno kompromisno rješenje koje je "podjednako dobro" ili "podjednako loše" za sve uzorke tog intervala.

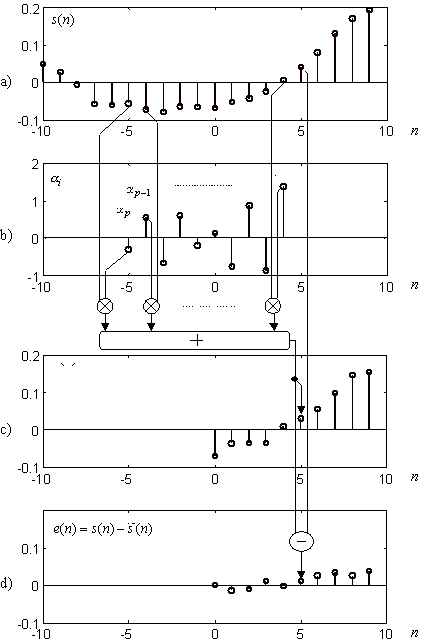
Slika

9.2‑1

a) uzorci promatranog signala, b) koeficijenti linearnog prediktora, c) linearna predikcija signala, d) pogreška predikcije

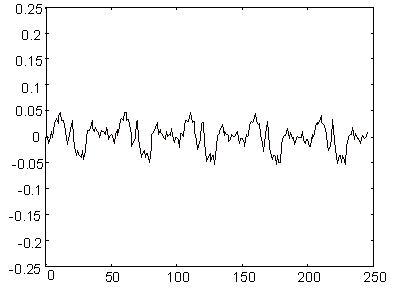
Na slici 9.2‑2 prikazani su originalni govorni signal za glasu 'u' i njegova linearna predikcija dobivena koeficijentima prediktora iz tablice 9.2‑1. Na slici je vidljivo vrlo dobro poklapanje ova dva signala, tj. predikcijska pogreška prikazana slikom 9.2‑3 vrlo je mala.

Za signale kod kojih je energija predikcijske pogreške značajno manja od energije polaznog signala kažemo da su korelirani, tj. imaju spektar koji nije ravan nego ima izražene maksimume. Postupak linearne predikcije je posebno učinkovit za takvu klasu signala, a govorni signal se obzirom na izraženu formantnu strukturu svakako ubraja u tu klasu (energija signala je u spektru lokalizirana u svega nekoliko rezonantnih karakteristika, tj. maksimuma). Glava tema narednih poglavlja bit će kako na osnovu snimljenih uzoraka govornog signala odrediti koeficijente "dobrih" prediktora koji "minimiziraju" predikcijsku pogrešku, te kako tako dobivene koeficijente prediktora dovesti u vezu s parametrima digitalnog modela vokalnog trakta predloženog u poglavljima 7 i 8.

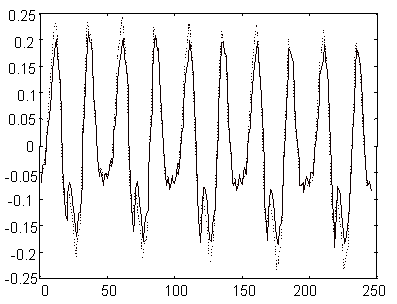
Slika

9.2‑2

Valni oblik promatranog signala (crtkano) i njegove linearne predikcije (punom linijom), glas 'u', fs=8kHz

Slika

9.2‑3

Pogreška predikcije za signal na slici 9.2‑2

1.3 Teoretske postavke analize linearnom predikcijom

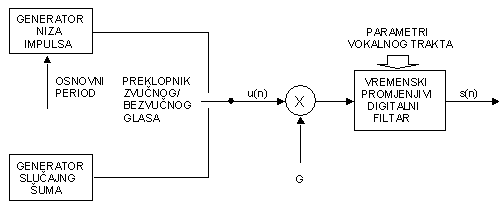
U poglavlju 8.5 uveden je potpuni digitalni model formiranja govornog signala, s blok shemom prikazanom na slici 8.5‑1. U svrhu diskusije postupka linearne predikcije pogodno je taj model pojednostaviti, kao što je prikazano na slici 9.3‑1. Kod ovog pojednostavljenog modela su utjecaji oblika glotalnog pulsa, prijenosne funkcije vokalnog trakta i zračenja na usnicama združeni u jednom sustavu i predstavljeni s vremenski promjenjivim digitalnim filtrom čija prijenosna funkcija H(z) ima oblik:

(9.3‑1)

Takav sustav je pobuđen nizom jediničnih impulsa za zvučne glasove ili sekvencom slučajnog šuma za bezvučne glasove. Prema tome parametri ovog modela su: položaj sklopke za odabir tipa pobude (zvučni ili bezvučni glas), period osnovne frekvencije titranja glasnica za zvučne glasove, faktor pojačanja i koeficijenti digitalnog filtra, a_k. Svi ovi parametri su, naravno, sporo promjenjivi s vremenom.

Slika

9.3‑1

Blok shema jednostavnog modela za formiranje govora

Zvučnost i period osnovne frekvencije mogu se odrediti korištenjem više različitih metoda, ali i pomoću onih temeljenih na analizi linearnom predikcijom. Kao što je već diskutirano, ovakav model koji ima samo polove predstavlja vrlo dobru reprezentaciju za zvučne ne‑nazalne glasove. U slučaju modeliranja nazalnih glasova ili zvučnih frikativa detaljna akustička teorija zahtijeva da prijenosna funkcija modela ima i nule, a ne samo polove, no biti će pokazano da će i ti glasovi biti reprezentirani dovoljno dobro ako je stupanj modela p dovoljno visok. Glavna prednost ovog pojednostavljenog modela s filtrom bez nula je u tome da se parametar pojačanja i koeficijenti a_k digitalnog filtra mogu na vrlo jednostavan i računski učinkovit način odrediti upravo korištenjem metode analize linearnom predikcijom.

Za sustav prikazan slikom 9.3‑1 i izrazom (9.3‑1) možemo pisati

(9.3‑2)

Iz izraza (9.3‑2) vidimo da su uzorci govora s(n) i pobude u(n) povezani jednostavnom jednadžbom diferencija:

(9.3‑3)

U prošlom poglavlju je uveden pojam linearnog prediktora s koeficijentima predikcije a_k, čija je blok shema prikazana na slici 9.3‑2. Jednadžba diferencija za ovaj prediktor dana u izrazu (9.2‑1) vrlo je slična jednadžbi diferencija (9.3‑3) pojednostavljenog modela sa slike 9.3‑1.

Slika

9.3‑2

Blok shema linearnog prediktora

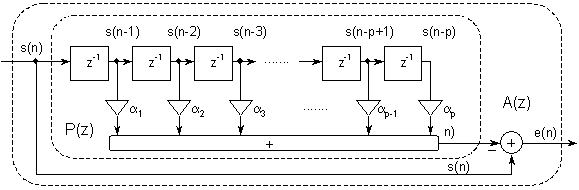
Prijenosna funkcija linearnog prediktora p-tog reda je polinom P(z) :

(9.3‑4)

Pogreška predikcije e(n) definirana je kao :

(9.3‑5)

Iz relacije (9.3‑5) može se uočiti da je niz uzoraka pogreške predikcije e(n) u stvari izlaz sustava A(z) prikazanog na slici 9.3‑2 čija prijenosna funkcija glasi

(9.3‑6)

Ako bi iz izraza (9.3‑5) izrazili s(n) kao funkciju prethodnih uzoraka s(n-k) i pogreške predikcije e(n) slijedi:

(9.3‑7)

Uspoređujući izraze (9.3‑3) i (9.3‑7) vidljivo je da su vrlo slični. Uz pretpostavku da je govorni signal stvarno nastao kao izlaz modela H(z) iz izraza (9.3‑1) i uz pretpostavku da su koeficijenti prediktora a_k jednaki koeficijentima modela a_k, tada će pogreška predikcije e(n) biti identički jednaka pobudnom signalu modela Gu(n). To drugim riječima znači da kada bi govorni signal s(n) propustili kroz sustav A(z), da bi se na njegovom izlazu dobio pobudni signal modela, pa se stoga A(z) često naziva inverzni filtar sustava tj. :

(9.3‑8)

Osnovni problem analize linearnom predikcijom je određivanje skupa koeficijenata prediktora {a_k} direktno iz uzoraka otipkanog govornog signala na takav način da se postigne dobro poklapanje kratkotrajnih spektralnih svojstava govornog signala i modela prema izrazu (9.3‑8) u čijem nazivniku figuriraju koeficijenti {a_k}. Zbog vremenski promjenjive prirode govornog signala, koeficijenti prediktora moraju biti određeni iz kratkog segmenta govornog signala unutar kojeg su spektralna svojstva signala stalna. Osnovna ideja linearne predikcije je pronalaženje takvih koeficijenata prediktora koji će minimizirati srednju kvadratnu pogrešku predikcije na tom promatranom segmentu govornog signala. Rezultirajući optimalni parametri {a_k} će zatim biti prihvaćeni kao koeficijenti polinoma u nazivniku modela H(z), tj. pretpostavit će se da su parametri modela {a_k} upravo jednaki tim određenim koeficijentima prediktora {a_k}.

Možda nije odmah uočljivo da će ovakav pristup dati zadovoljavajuće rezultate, ali on se može opravdati na nekoliko načina. Prvo, uz pretpostavku da stvarno vrijedi uvjet da je a_k=a_k, tada je e(n)=Gu(n). Za zvučni govor ovo bi značilo da se e(n) sastoji od niza impulsa, tj. e(n) bi uglavnom bio jednak nuli i imao bi malu energiju. Stoga, čini se da je pronalaženje parametara {a_k} koji minimiziraju energiju pogreške predikcije u skladu s gore izloženim opažanjima.

Drugo objašnjenje je čisto matematičke prirode. Uz pretpostavku da vremenski nepromjenjiv sustav H(z) prema izrazu (9.3‑1) s poznatim koeficijentima {a_k} pobudimo s jediničnim impulsom ili sa stacionarnim bijelim šumom, te ako na uzorcima njegovog odziva provedemo postupak linearne predikcije, tada će tako dobiveni optimalni koeficijenti prediktora {a_k} biti jednaki polaznim koeficijentima sustava {a_k}. Identička jednakost vrijedi u slučaju pobude s jediničnim impulsom, dok u slučaju pobude sa stacionarnim bijelim šumom koeficijenti {a_k} teže prema {a_k}, a poklapanje je to bolje što je broj uzoraka signala veći.

Treće opravdanje za korištenje minimalne srednje kvadratne pogreške predikcije kao osnove za određivanje parametara modela je čisto praktične prirode, tj. uz tako definiranu ciljnu funkciju optimalni koeficijenti prediktora se nalazi kao rješenje običnog skupa linearnih jednadžbi. Još važnije je da rezultirajući parametri veoma dobro modeliraju kratkotrajna spektralna svojstva govornog signala kako će biti pokazano.

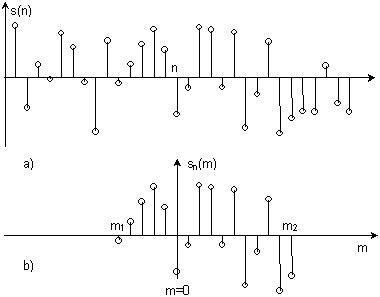
Postupak određivanja koeficijenata prediktora provodi se nad vremenskim segmentom govornog signala konačnog trajanja. Taj segment biti će označen sa s_n(m), a radi se o dijelu signala s(n) u okolini indeksa n, gdje je ta okolina određena rasponom indeksa m, tj. vrijedi:

(9.3‑9)

Ta operacija izdvajanja segmenta signala ilustrirana je na slici 9.3‑3, gdje se indeks m kreće od m₁ do m₂

Srednja vrijednost pogreške predikcije na tako odabranom segmentu signala s_n(m) definirana je kao :

(9.3‑10) (9.3‑11) (9.3‑12)

Granice sumacija u izrazima (9.3‑10) do (9.3‑12) su privremeno ostavljene nedefinirane, tj. naznačeno je samo da se sumacija provodi preko indeksa m. Raspon ove sumacije ovisiti će o tipu predikcijskog postupka, ali u svakom slučaju radi se o konačnom rasponu. Stroga definicija srednje vrijednosti zahtijeva da se izrazi (9.3‑10) do (9.3‑12) podijele se brojem uzoraka u tom konačnom intervalu, no taj faktor skale neće utjecati na rješenje, tj. optimalni skup koeficijenta a_k koji minimiziraju E_n ne ovisi o tom faktoru skale.

Slika

9.3‑3

Govorni signal s(n) a), Izdvojeni segment sn(m) u okolini indeksa n b)

Vrijednosti parametara a_k koji minimiziraju E_n prema relaciji (9.3‑12) mogu se odrediti tako da se parcijalne diferencijalne jednadžbe E_n po nepoznatim koeficijentima izjednače s nulom, tj. , za i=1,2, ..., p. Lako je pokazati da iz ovog uvjeta slijedi sustav od p linearnih jednadžbi po nepoznanicama a₁ do a_p oblika:

(9.3‑13)

Primjer izvoda ovog sustava biti će prikazan za slučaj linearnog prediktora drugog reda (p=2). Srednja kvadratna pogreška predikcije E_n definirana je kao :

(9.3‑14)

Izjednačavanjem parcijalnih diferencijalnih jednadžbi s nulom slijedi:

(9.3‑15) (9.3‑16)

odnosno nakon dijeljenja s 2 i separacije nepoznanica i konstanti :

(9.3‑17) (9.3‑18)

Usporedbom ovog sustava s općom formom danom u izrazu (9.3‑13) vidljivo je poklapanje. Sustav jednadžbi moguće je i kompaktnije zapisati ako se definira:

(9.3‑19)

tada izraz (9.3‑13) možemo kraće pisati kao :

(9.3‑20)

ili u matričnom obliku:

(9.3‑21)

Rješavanjem ovog sustava jednadžbi slijedi skup optimalnih koeficijenata prediktora {a_k} koji minimizira srednju kvadratnu pogrešku predikcije E_n za segment s_n(m). Naravno da i ovi koeficijenti ovise o indeksu n za koji je proveden postupak, ali to neće biti posebno naglašavano dodavanjem indeksa na koeficijente a_k.

Korištenjem izraza (9.3‑12) i (9.3‑13) može se pokazati da se minimalna srednja kvadratna vrijednost pogreške predikcije uz koeficijente a_k koji zadovoljavaju sustav (9.3‑21), može odrediti kao:

(9.3‑22)

odnosno uz korištenje izraza (9.3‑19) za f_n(i,k) u kompaktnoj formi oblika:

(9.3‑23)

Dakle, ukupna minimalna pogreška sastavljena je od fiksne komponente f_n(0,0) i od komponenata koje ovise o koeficijentima predikcije. Ovaj fiksni dio f_n(0,0) je u stvari jednak energiji segmenta ulaznog signala s_n(m).

Da bi se odredili optimalni koeficijenti predikcije, treba prvo odrediti pomoćne varijable f_n(i,k) i to za one kombinacije i i k koje se javljaju su sustavu jednadžbi (9.3‑21), tj. za 1 £ i £ p i 0 £ k £ p. Nakon toga treba još jedino riješiti sustav (9.3‑21) čime se nalaze optimalni koeficijenti prediktora {a_k}. Iako iz izloženog izgleda da je analiza linearnom predikcijom u principu vrlo jednostavna, ipak su detalji izračunavanja f_n(i,k) i proizlazećih rješenja jednadžbi prilično komplicirani i zahtijevaju daljnju diskusiju.

Do sada još uvijek nije fiksiran raspon sumacije po indeksu m, no valja napomenuti da je on jednak u svim izrazima u kojima figurira suma po m. Naravno, zbog vremenske promjenjivosti spektralnih svojstava govornog signala, taj raspon mora biti konačan. Postoje dva osnovna pristupa odabiru ovog raspona i kao što će biti prikazano u narednim poglavljima, dva postupka linearne predikcije će se razlikovati samo po tome kako je odabran taj raspon, odnosno na koji način se provodi izdvajanje segmenta s_n(m) iz govornog signala s(n).