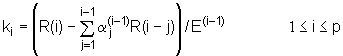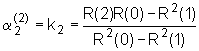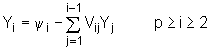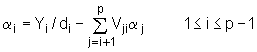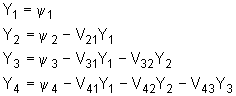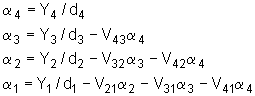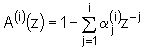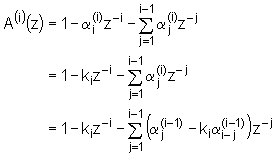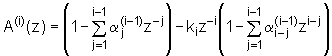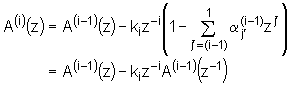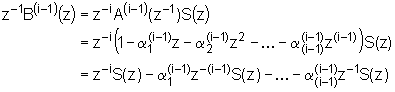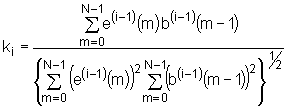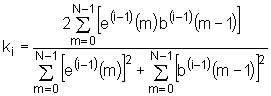1

1.1 Postupci rješavanja sustava LPC jednadžbi

Obzirom da se postupak analize govornog signala primjenom linearne predikcije često koristi u sustavima koji rade u stvarnom vremenu, potrebno je postupak izračunavanja prediktora provesti što je moguće učinkovitije. Iako je u tu svrhu moguće primijeniti bilo koji poznati postupak rješavanja linearnog sustava jednadžbi, postoje značajne razlike u njihovoj učinkovitosti, tj. neki su jednostavniji i brži, dok su drugi složeniji i sporiji. Zbog posebnih svojstava matrice koeficijenata sustava, rješenje je moguće naći puno učinkovitije nego u općenitom slučaju. U ovom poglavlju biti će predstavljena i detaljno analizirana dva takva učinkovita postupka, od kojih se prvi odnosi na autokorelacijsku metodu, dok se drugi primjenjuje u slučaju upotrebe metode kovarijance. Diskutirat će se i svojstva dobivenih prediktora.

1.1.1 Durbinov rekurzivni postupak za rješavanje autokorelacijskih jednadžbi

Matrični oblik sustava jednadžbi za izračunavanje koeficijenata prediktora autokorelacijskom metodom ima oblik:

(9.7‑1)

Koristeći svojstva Toeplitz-ove strukture koju posjeduje matrica sustava jednadžbi, razvijeno je nekoliko učinkovitih rekurzivnih algoritama za rješavanje gornjeg sustava jednadžbi. Premda su Levinson-Robinson‑ovi algoritmi najpopularniji i najpoznatiji, najučinkovitiji od poznatih postupaka za rješavanje ovakvog sustava jednadžbi je Durbin-ov rekurzivni algoritam koji se može opisati na sljedeći način (zbog jednostavnosti zapisa izostavljen je indeks n kod autokorelacijske funkcije R i pogreške predikcije E) :

	(9.7‑2)
	(9.7‑3)
	(9.7‑4)
	(9.7‑5)
	(9.7‑6)

Jednadžbe od (9.7‑3) do (9.7‑6) rješavaju se rekurzivno za i=1,2,....,p pa je konačno rješenje dano u obliku:

(9.7‑7)

Može se uočiti da su u postupku izračunavanja koeficijenata za prediktor reda p također dobiveni i svi koeficijenti za prediktore nižeg reda, tj. a_j⁽ⁱ⁾ je j-ti koeficijent prediktora reda i.

Za ilustraciju gornjeg postupka, može se razmotriti primjer izračunavanja koeficijenata prediktora drugog reda. Izvorna matrična jednadžba ima sljedeći oblik:

Koristeći izraze (9.7‑2) do (9.7‑7)dobivamo:

Treba uočiti da vrijednost E⁽ⁱ⁾ u izrazu (9.7‑6) predstavlja pogrešku predikcije za prediktor reda i. Moguće je stoga, u svakom koraku rekurzivnog postupka pratiti pogrešku predikcije za prediktor reda i. Isto tako, ako se koeficijenti autokorelacije R(k) zamijene skupom normaliziranih autokorelacijskih koeficijenata, tj. r(k)=R(k)/R(0), tada rješenje matrične jednadžbe ostaje nepromijenjeno. Međutim, pogreška E⁽ⁱ⁾ se onda interpretira kao normalizirana pogreška predikcije. Ako se ta normalizirana pogreška označi sa V⁽ⁱ⁾ tada vrijedi:

(9.7‑8)

gdje je:

(9.7‑9)

Obzirom da je R(0) jednak energiji izdvojenog segmenta govornog signala, V⁽ⁱ⁾ definira koliko je puta energija predikcijske pogreške manja od ulazne energije signala. Normalizirana pogreška predikcije prediktora nultog reda V⁽⁰⁾ jednaka je 1, jer se predikcija uopće ne provodi, dok se povećanjem reda prediktora V⁽ⁱ⁾ smanjuje prema nuli, tj. vrijedi V⁽ⁱ⁺¹⁾£V⁽ⁱ⁾. U postupku predikcije poželjno je što je moguće više smanjiti energiju predikcijske pogreške u odnosu na ulaznu energiju. Dobitak uslijed linearne predikcije se često izražava u dB, prema izrazu:

(9.7‑10)

Može se pokazati da se normalizirana pogreška predikcije za i=p može zapisati i u obliku:

(9.7‑11)

gdje su k_i pomoćne varijable dobivene u Durbin-ovom rekurzivnom postupku koje su uvijek u slijedećim granicama:

(9.7‑12)

Ovaj uvjet za parametre k_i je važan jer predstavlja nužan i dovoljan uvjet da svi korijeni polinoma A(z) budu unutar jedinične kružnice čime se osigurava stabilnost sustava H(z). Treba dodati da kod metode kovarijance koja će biti opisana u narednim poglavljima ne postoji ovakav uvjet koji bi garantirao stabilnost sustava.

1.1.2 Primjer izračunavanja prediktora Durbinovim algoritmom

Durbinov algoritam uzima u obzir činjenicu da su elementi unutar svih desno položenih dijagonala matrice autokorelacije jednaki (Toeplitz-ova struktura), te je za njegovu izvedbu potrebno poznavati samo autokorelacijske koeficijente od R(0) do R(p). Provedbom gore opisanog rekurzivnog algoritma dobivamo izlaznu matricu koeficijenata linearnog prediktora u kojoj su pohranjeni koeficijenti ne samo za prediktor reda p nego i za sve prediktore od prvog do p‑tog reda. Za konkretan primjer linearnog prediktora 10. reda, dobiva se matrica prikazana u tablici 9.7‑1. Treba napomenuti da su elementi na glavnoj dijagonali upravo jednaki koeficijentima k₁ do k₁₀.

Pored matrice koeficijenata linearnog prediktora ovim algoritmom se dobiva i vektor pogreške predikcije E čijim je praćenjem moguće utvrditi dovoljan red prediktora. Brzina s kojom se E⁽ⁱ⁾ smanjuje s povećanjem reda prediktora nije jednaka, tj. ovisi o i, a naravno ovisi i o glasu čija se predikcija provodi. Ispočetka se E⁽ⁱ⁾ smanjuje relativno naglo, dok nakon nekog stupnja i dobitak uslijed povećanja reda prediktora više nije toliko značajan.

Tablica

9.7‑1

Koeficijenti linearnog prediktora za prediktore reda 1. do 10.

RED
1.	0.75	-	-	-	-	-	-	-	-	-
2.	1.41	-0.89	-	-	-	-	-	-	-	-
3.	1.44	-0.93	0.03	-	-	-	-	-	-	-
4.	1.43	-0.62	-0.46	0.34	-	-	-	-	-	-
5.	1.52	-0.74	-0.62	0.72	-0.27	-	-	-	-	-
6.	1.44	-0.52	-0.81	0.50	0.19	-0.30	-	-	-	-
7.	1.46	-0.53	-0.84	0.55	0.23	-0.40	0.07	-	-	-
8.	1.47	-0.60	-0.81	0.64	0.09	-0.49	0.30	-0.16	-	-
9.	1.52	-0.69	-0.65	0.61	-0.11	-0.24	0.49	-0.62	0.31	-
10.	1.52	-0.70	-0.65	0.61	-0.11	-0.23	0.48	-0.63	0.33	-0.01

Na slici 9.7‑1 prikazane su amplitudno frekvencijske karakteristike |H(e^j^W)| koje su dobivene korištenjem linearnih prediktora od prvog do desetog reda (prvi red je na dnu, a zatim redovi rastu prema gore) međusobno pomaknute za 20 dB radi bolje preglednosti, a na samom vrhu prikazan je spektar signala koji se modelira. Lako se uočava da sa povećanjem reda prediktora prijenosne funkcije H(z) sve bolje slijede formantnu strukturu spektra originalnog signala. Iako je pogreška predikcije do sada bila izražavana samo u vremenskoj domeni, kao suma kvadrata razlike stvarnog i predviđenog signala, ta se ista pogreška može definirati i u spektralnoj domeni. Bit će pokazano da se to svodi na izračunavanje integrala kvocijenta spektra snage signala, |S_n(e^j^W)|² i kvadrata amplitudno frekvencijske karakteristike modela, |H(e^j^W)|². Uistinu, vidljivo je da se povećanjem reda predikcije prijenosna funkcija modela po obliku sve više približava obliku spektra signala tj. sve ga bolje modelira.

Slika

9.7‑1

Prikaz prijenosnih funkcija za različite redove prediktora

1.1.3 Računanje prediktora za metodu kovarijance Cholesky dekompozicijom

Kod metode kovarijance, sustav jednadžbi kojeg treba riješiti je oblika:

(9.7‑13)

ili u matričnom obliku

(9.7‑14)

gdje je F pozitivno definitna simetrična matrica koja u i-tom retku i j-tom stupcu ima element f_n(i,j), dok su a i y stupci (vektori) sa elementima odnosno f_n(i,0) (i predstavlja indeks retka). Sustav jednadžbi, dan izrazom (9.7‑13) može biti učinkovito riješen, budući da je matrica F simetrična i pozitivno definitna matrica. Metoda rješavanja koja se može primijeniti na takve matrice naziva se dekompozicija Choleskog, a ponekad se naziva i metoda drugog korijena. Osnovna ideja te metode je rastavljanje matrice F u produkt tri matrice, tj., prema izrazu:

(9.7‑15)

gdje je V donja trokutasta matrica (svi elementi glavne dijagonale imaju iznos 1), dok je D dijagonalna matrica. Oznaka ^T označava matričnu transpoziciju. Elementi matrica V i D se lako i jednoznačno određuju direktno iz izraza (9.7‑15). Raspisivanjem tog izraza za element f_n(i,j) u i-tom retku i j-tom stupcu matrice F dobiva se slijedeći odnos:

(9.7‑16)

Obzirom da su svi dijagonalni elementi matrice V jednaki 1, izdvajanjem zadnjeg člana sume u gornjem izrazu slijedi:

(9.7‑17)

Specijalno za dijagonalne elemente ,f_n(i,i), izraz je još jednostavniji i slijedi :

(9.7‑18)

odnosno,

(9.7‑19)

Inicijalna vrijednost za i=1 dana je sa:

(9.7‑20)

Da ilustriramo korištenje jednadžbi (9.7‑15) do (9.7‑20) razmotriti ćemo primjer sa p = 4 i matričnim elementima kraće označenim sa f_ij = f_n(i,j). Jednadžba (9.7‑15) je prema tome oblika :

Da izračunamo d₁ do d₄ i V_ij, počinjemo sa jednadžbom (9.7‑20). Za i = 1 dobivamo prvi dijagonalni element matrice D, tj., :

Koristeći jednadžbu (9.7‑17) za i = 2,3,4 računamo V₂₁, V₃₁ i V₄₁, tj. određujemo prvi stupac matrice V, iz čega slijedi:

Sada korištenjem rezultata iz prethodnog koraka, primjenom jednadžbe (9.7‑19), za i = 2 nalazimo slijedeći dijagonalni element matrice D :

Ponovnom primjenom jednadžbe (9.7‑17) za i = 3 i 4 nalazimo elemente drugog stupca matrice V:

odnosno:

Jednadžba (9.7‑19) se sada koristi uz i = 3 za izračunavanje d₃, zatim se jednadžba (9.7‑17) koristi uz i = 4 za izračunavanje V₃₄, te se konačno jednadžba (9.7‑19) koristi uz i = 4 za izračunavanje d₄. Iz ovog je vidljivo da se u tom postupku naizmjence nalazi po jedan dijagonalni element matrice D i po jedan stupac matrice V.

Nakon što se odrede matrice V i D izračunavanje vektora a je vrlo jednostavno i provodi se primjenom dvokoračnog postupka. Kombiniranjem izraza (9.7‑14) i (9.7‑15) dobivamo :

(9.7‑21)

što može biti prikazano i u obliku

(9.7‑22)

gdje je Y pomoćni stupac koji određuje rješenje sustava po a, tj. :

(9.7‑23)

odnosno, :

(9.7‑24)

Zbog donje trokutaste forme matrice V, određivanje pomoćnog stupca Y na osnovu matrice V i stupca y prema izrazu (9.7‑22) vrlo je jednostavno i moguće je provesti korištenjem rekurzivne formule oblika :

(9.7‑25)

s početnom jednakosti:

(9.7‑26)

Nakon određivanja pomoćnog stupca Y, provodi se množenje s D^‑1, kao što zahtijeva izraz (9.7‑24), no obzirom da je matrica D dijagonalna, ovo se svodi na obično dijeljenje elemenata stupca Y s dijagonalnom elementima matrice D (prvi s prvim, drugi s drugim itd.). Zbog gornje trokutaste forme matrice V^T i izraz (9.7‑24) se može rekurzivno riješiti po elementima stupca a koristeći slijedeći izraz:

(9.7‑27)

s početnom jednakosti:

(9.7‑28)

Treba napomenuti da indeks i u jednadžbi (9.7‑27) ide unazad od i = p‑1 do i = 1. Da ilustriramo upotrebu izraza (9.7‑25) do (9.7‑28), nastavljamo prethodni primjer i najprije određujemo vrijednosti pretpostavljajući da su V i D već određeni i poznati. U matričnom obliku imamo jednadžbu :

Iz jednadžbi (9.7‑26) i (9.7‑25) dobivamo :

Sa izračunatim vrijednostima rješavamo jednadžbu (9.7‑24) koja je oblika

Iz jednadžbi (9.7‑28) i (9.7‑27) dobivamo :

što ujedno predstavlja konačno rješenje za linearni sustav jednadžbi metode kovarijance.

Upotreba postupka dekompozicije Choleskog vodi ka vrlo jednostavnom izrazu za minimalnu pogrešku predikcije izraženu kao funkcija pomoćnog stupca Y i matrice D. Prisjećamo se da izraz za minimalnu pogrešku predikcije u slučaju upotrebe metode kovarijance, glasio:

(9.7‑29)

ili u matričnoj notaciji :

(9.7‑30)

Prema izrazu (9.7‑24), a^T je moguće zamijeniti sa pa slijedi :

(9.7‑31)

Koristeći jednadžbu (9.7‑22) dobivamo

(9.7‑32)

odnosno :

(9.7‑33)

Prema tome, minimalna srednja kvadratna pogreška predikcije , koja se postiže uz primjenu optimalnog prediktora, može biti određena direktno iz stupca Y i dijagonalne matrice D. Nadalje, izraz (9.7‑33) se može koristiti za izračunavanje vrijednosti i za prediktore svih nižih redova, (od 1 do p‑1) jednostavnim skraćivanjem sume u izrazu (9.7‑33) do željenog stupnja p. Na osnovu toga je moguće pratiti kako se energija predikcijske pogreške smanjuje s povećanjem reda prediktora, te odabrati potrebni red.

1.2 Predikcija mrežastom (lattice) strukturom

Dva do sada opisana pristupa izračunavanju koeficijenata linearnog prediktora su: metoda kovarijance i metoda autokorelacije koje se obje provode u dva osnovna koraka:

1) računanje matrice korelacijskih vrijednosti (R ili F) i

2) izračunavanje rješenja sustava linearnih jednadžbi.

Iako se navedene metode često i uspješno koriste u primjenama vezanim uz obradu govora, postoji još jedan pristup problemu linearne predikcije koji se naziva predikcija mrežastom strukturom (engl. lattice method). Kod ove metode su oba koraka izračunavanja prediktora objedinjena u formi rekurzivnog postupka. Oba pristupa imaju zajedničku osnovu, a njihovu vezu je najlakše ilustrirati primjenom Durbinovog algoritma. U i-tom koraku tog rekurzivnog postupka, Durbinov algoritam rezultira s koeficijentima optimalnog linearnog prediktora i-tog stupnja . Koristeći te koeficijente možemo definirati prijenosnu funkciju inverznog filtra i-tog reda:

(9.8‑1)

Ako je ovaj filtar pobuđen sa segmentom govornog signala s_n(m)=s(n+m)w(m), tada će na njegovom izlazu biti pogreška predikcije, gdje je:

	(9.8‑2)
	(9.8‑3)

Radi jednostavnosti zapisa namjerno je ispušten indeks n koji označava segment signala i predikcijske pogreške u okolini uzorka n. Predikcija uzorka s(m) primjenom prediktora reda i označena je sa (značenje sufiksa _f biti će objašnjeno kasnije). Ako na izraz (9.8‑2) primijenimo z‑transformaciju vrijedi:

(9.8‑4)

U Durbin‑ovom postupku pokazano je kako se na osnovu koeficijenata prediktora stupnja (i-1) i koeficijenta k_i određuju koeficijenti prediktora i-tog stupnja tj. vrijedi:

za j=1,2,......,i-1.

(9.8‑5)

Ako bi ovaj izraz uvrstili u prijenosnu funkciju inverznog filtra (9.8‑1) tada slijedi:

(9.8‑6)

odnosno, rastavljanjem na dvije sume :

(9.8‑7)

U prvom članu prepoznajemo prijenosnu funkciju prediktora reda (i-1), tj. A^(i‑1)(z), dok ćemo drugi član malo modificirati, tako da indeks sumacije j, zamijenimo sa j'=i‑j, pa slijedi:

(9.8‑8)

Treba naglasiti da prijenosna funkcija prediktora A^(i‑1) u drugom članu ima argument z^‑1, a ne z kao što je to u prvom članu. Uvrštavajući izraz (9.8‑8) u izraz (9.8‑4) dobivamo:

(9.8‑9)

Prvi dio izraza (9.8‑9) je očito z-transformacije pogreške predikcije za prediktor reda . Drugi dio izraza se može malo modificirati tako da izlučimo k_iz^‑1, pa slijedi :

(9.8‑10)

Član u zagradi označen je sa B^(i-1)(z), tj. općenito vrijedi:

(9.8‑11)

Smisao ovog člana lakše je shvatiti ako se odredi inverzna z-transformacija od koji nakon raspisivanja glasi:

(9.8‑12)

Nakon prebacivanja u vremensku domenu slijedi:

(9.8‑13)

Iz izraza (9.8‑13) može se prepoznati da predstavlja pogrešku predikcije unazadnog prediktora reda (i‑1) (engl. backward prediction error sequence) koji provodi predikciju uzorka s(m-i) na osnovu i‑1 uzoraka koji slijede, tj. na osnovu {s(m-i+j), za j=1,2,....,i-1}. Ta unazadna predikcija označena je sa , gdje sufiks _b dolazi od backward (unazad). Treba naglasiti da ovaj unazadni prediktor koristi iste koeficijente kao i normalni unaprijedni prediktor reda (i-1), koji provodi predikciju uzorka s(m) označenu sa na osnovu i‑1 uzoraka koji mu prethode, tj. na osnovu {s(m-j), za j=1,2,....,i-1} (sufiks _f dolazi od forward (unaprijed)). Taj unaprijedni prediktor odgovara prvom članu u izrazima (9.8‑8) i (9.8‑10), a njegova pogreška predikcije označena je sa e^(i‑1)(m). Interesantno je uočiti da se predikcija u oba slučaja provodi na osnovu istih uzoraka signala i na osnovu istih koeficijenata prediktora, jedino što se u prvom slučaju predviđa uzorak s(m-i), a u drugom slučaju uzorak s(m). Razlika je i u tome što je redoslijed koeficijenata obrnut, tj. u prvom slučaju množi uzorak s(m‑i+1), dok u drugom slučaju taj se koeficijent množi sa s(m‑1).

Uz ovako definiranu unaprijednu i unazadnu pogrešku predikcije prediktora reda (i-1), lako je pokazati da se inverznom z-transformacijom izraza (9.8‑10) dobiva slijedeća jednadžba diferencija za pogrešku predikcije unaprijednog prediktora reda i, :

(9.8‑14)

Drugim riječima, pogrešku predikcije unaprijednog prediktora i-tog reda moguće je odrediti na osnovu unaprijedne i unazadne pogreške prediktora reda (i-1) i na osnovu poznavanja koeficijenta k_i=a_i⁽ⁱ⁾.

Opisana zakonitost ilustrirana je i na slici 9.8‑1, gdje su prikazana sva tri prediktora: unaprijedni prediktor reda (i) (na vrhu), unaprijedni prediktor reda (i-1) (u sredini) i unazadni prediktor reda (i-1) (na dnu). Pogrešku predikcije e⁽ⁱ⁾(m) moguće je dobiti bilo kao izlaz prvog prediktora, bilo kombiniranjem pogreški e^(i‑1)(m) i b^(i‑1)(m‑1) prema izrazu (9.8‑14).

Slika

9.8‑1

Ilustracija predikcije unaprijed i predikcije unazad koristeći prediktore reda (i-1)

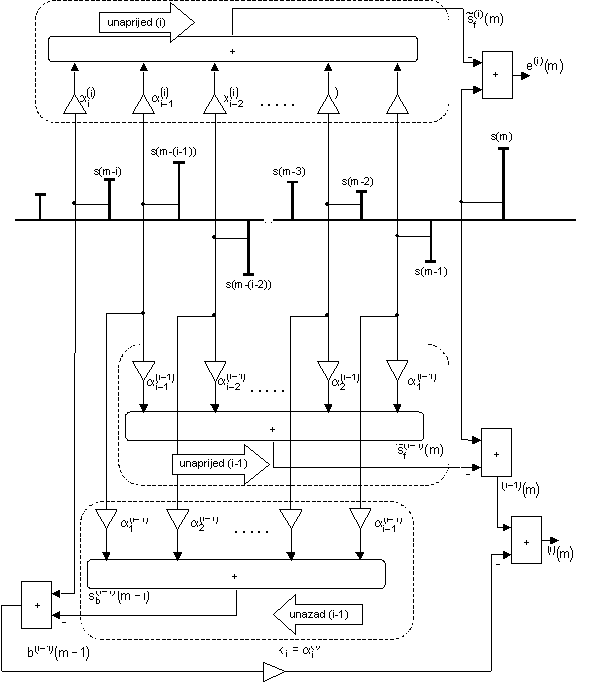
Slična zakonitost vrijedi i za unazadnu pogrešku prediktora reda i, označenu sa b⁽ⁱ⁾(m). To je moguće pokazati uvrštavanjem izraza (9.8‑8) u (9.8‑11) nakon čega dobivamo:

(9.8‑15)

odnosno :

(9.8‑16)

Prebacivanjem u vremensku domenu slijedi da se unazadna pogreška predikcije prediktora reda i, također može odrediti kombiniranjem unaprijedne i unazadne pogreške prediktora reda (i-1), tj. :

(9.8‑17)

Izrazi (9.8‑14) i (9.8‑17) predstavljaju svojevrsnu rekurzivnu formulu kojom je moguće na osnovu predikcijske pogreške prediktora nižeg reda odrediti unaprijednu i unazadnu predikcijsku pogrešku prediktora prvog višeg reda. Kao i kod svake rekurzivne formule, potrebno je definirati inicijalnu vrijednost za slučaj i=0, tj. za slučaj kada se predikcija uopće ne provodi. Tada vrijedi:

(9.8‑18)

tj. predikcijske pogreške su jednake ulaznom signalu s(m).

Rekurzivne formule (9.8‑14) i (9.8‑17) možemo prikazati i pomoću grafa toka signala na slici 9.8‑2. Takva struktura se naziva mrežastom (engl. lattice) strukturom. Ako mrežu proširimo na p sekcija, tada izlaz iz posljednje gornje grane na slici 9.8‑2 predstavlja unaprijednu pogrešku predikcije prediktora p‑tog reda. Slika 9.8‑2 u stvari prikazuje još jednu moguću izvedbu inverznog filtra (engl. prediction error filter) čija je prijenosna funkcija A(z) dana izrazom (9.8‑1) uz i=p.

Potrebno je naglasiti da je mrežasta struktura na slici 9.8‑2 direktna posljedica primjene Durbin‑ovog algoritma i parametara k_i dobivenih izrazima (9.7‑2) do (9.7‑7). Koeficijenti predikcije {a_j^(p), j=1,2,..,p} nigdje ne figuriraju eksplicitno na slici 9.8‑2, već indirektno preko parametara k_i. Itakura je pokazao da se optimalni parametri k_i mogu odrediti direktno na osnovu unaprijedne i unazadne pogreške predikcije prediktora reda i-1, a zbog prirode mrežaste strukture taj se postupak može provesti rekurzivno za sve koeficijente {, i=1,2,.......,p} bez da se eksplicitno izračunaju koeficijenti {a_j^(p), j=1,2,..,p}.

Slika

9.8‑2

Blok dijagram izvedbe inverznog filtra A(z) mrežastom (lattice) strukturom

To se provodi korištenjem slijedećeg izraza:

(9.8‑19)

Ovaj izraz je oblika normalizirane kros‑korelacijske funkcije koja mjeri sličnost unaprijedne i unazadne pogreške predikcije prediktora reda (i‑1). Zbog toga se koeficijenti uobičajeno nazivaju koeficijentima parcijalne korelacije ili kraće PARCOR koeficijentima, a nekad se i nazivaju samo k-parametri.

Izraz (9.8‑19) zamjenjuje izraz (9.7‑3) u Durbin‑ovom algoritmu, a ako je baš potrebno koeficijenti prediktora, a_j^(p), se i dalje mogu izračunati rekurzivno iz koeficijenata k_i kao i prije. Određivanje optimalnih koeficijenata prediktora prema izrazu (9.8‑19) se naziva PARCOR analiza. Takav pristup predstavlja alternativu klasičnim postupcima kod kojih se u svrhu izračunavanja prediktora mora provesti inverzija matrice. Rezultati koji se dobivaju ovakvim postupkom su identični onima koji bi se dobili autokorelacijskom metodom, tj. niz PARCOR koeficijenata je određen tako da minimizira srednju kvadratnu pogrešku predikcije unaprijed. Najvažnije od svega je da ovakav pristup otvara jednu cijelu novu klasu postupaka temeljenih na mrežastoj strukturi.

1.2.1 Burgov algoritam

U dosadašnjim razmatranjima koeficijenti prediktora k_i određivani su tako da minimiziraju isključivo srednju kvadratnu pogrešku unaprijedne predikcije. Burg je predložio modifikaciju tog postupka, kod koje se minimizira suma srednje kvadratne pogreške unaprijedne i unazadne predikcije sa slike 9.8‑2, tj. prema izrazu:

(9.8‑20)

Uvrstimo li izraze (9.8‑14) i (9.8‑17) u izraz (9.8‑20), te ako odredimo parcijalnu derivaciju po koeficijentu k_i dobivamo:

(9.8‑21)

Izjednačimo li parcijalnu derivaciju s nulom i riješimo po k_i slijedi:

(9.8‑22)

Slično kao i kod Durbin‑ovog algoritma, ako su koeficijenti k_i izračunati korištenjem izraza (9.8‑22) tada i dalje vrijedi: , što garantira stabilnost LPC filtra. Naravno treba imati u vidu da će se ovi k_i koeficijenti razlikovati od onih određenih izrazom (9.8‑19), koji su u stvari identični koeficijentima koji se dobivaju autokorelacijskim postupkom.

Na kraju ponovimo ukratko koji su koraci korišteni za izračunavanje optimalnih koeficijenata predikcije i k‑parametara:

1) Inicijalizacija: .

2) Izračunavanje prema izrazu (9.8‑22)

3) Određivanje pogrešaka predikcije unaprijed i unazad izrazima (9.8‑14) i (9.8‑17)

4) Postavi i=2.

5) Određivanje izrazom (9.8‑22).

6) Određivanje za j=1,2,.....,i-1 iz izraza (9.7‑5), (prema potrebi)

7) Određivanje i iz izraza (9.8‑14) i (9.8‑17).

8) Povećaj i za jedan.

9) Ako je i manje ili jednako p vrati se na korak 5).

10) Inače .... procedura je završena.

Vidjeli smo da postoji nekoliko razlika između izvedbe predikcije mrežastom strukturom i izvedbe metodama kovarijance ili autokorelacije, no osnovna razlika je u tome što se mrežastom metodom predikcijski koeficijenti računaju direktno iz uzoraka govora bez posrednog računanja korelacijskih funkcija. Istovremeno metoda jamči stabilan filtar i bez korištenja vremenskog otvora koji je nužan kod metode autokorelacije. Iz tih je razloga formulacija linearne predikcije mrežastom strukturom ostala važan i opravdan pristup u analizi govora linearnom predikcijom.