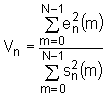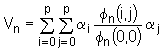1.1 Signal predikcijske pogreške
Nusproizvod LPC analize je određivanje signala
pogreške 
, definiranog kao:
|
|
(9.10‑1) |
Ako je stvarni govorni signal generiran sustavom koji se može dobro modelirati vremenski promjenjivim prediktorom reda p, tada je e(n) jednako dobra aproksimacija pobudnog signala tog sustava.
Takvim razmišljanjem može se očekivati da će predikcijska pogreška biti velika (za zvučni govor) na početku svakog pitch perioda. Stoga se pitch period može odrediti pomoću pozicija uzoraka e(n) koji imaju veliku amplitudu, to jest pitch period se može definirati kao vremenski razmak između parova uzoraka e(n) čija amplituda prelazi određeni prag. Inače, pitch period se može procijeniti i izračunavanjem autokorelacijske funkcije signala predikcijske pogreške e(n) i detekcijom najvišeg vrha u odgovarajućem opsegu pomaka. Korisnost signala predikcijske pogreške e(n) u određivanju pitch perioda može se tumačiti i time da je spektar signala predikcijske pogreške približno ravan, iz čega slijedi da su efekti formanata uklonjeni iz signala predikcijske pogreške, što omogućava točniju estimaciju pitch perioda.
Za ilustraciju prirode signala predikcijske pogreške, slika 9.10‑1 prikazuje niz odsječaka valnih oblika nekoliko samoglasnika i pripadajućih signala predikcijskih pogrešaka e(n). Za ove jednostavne zvukove samoglasnika, signal predikcijske pogreške e(n) ima oštre pulseve na razmacima koji odgovaraju pitch periodu tih samoglasnika.
|
Slika |
Tipični signali i spektri za LPC metodu kovarijance, za muškog govornika, p = 14, N = 200 |
|
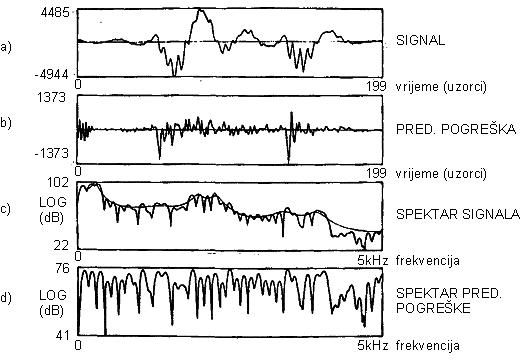
Slika |
Tipični signali i spektri za LPC autokorelacijsku metodu sa Hamming-ovim vremenskim otvorom, za muškog govornika, p = 14, N = 200 |
Dodatni primjeri signala predikcijske pogreške e(n) prikazani su na slikama 9.10‑2 do 9.10‑5. Na svakoj od ovih slika (a) dio prikazuje odsječak
signala koji se analizira, dio (b) prikazuje rezultirajući signal predikcijske
pogreške e(n), dio (c) prikazuje modul DFT-a
signala iz (a) dijela slike izražen u [dB] sa superponiranim modulom
frekvencijske karakteristike H(ejwT) sustava 
, dok dio (d) prikazuje amplitudni spektar signala
predikcijske pogreške e(n), također izražen u [dB].
Na slikama 9.10‑2 i 9.10‑3 prikazana je analiza 20 ms samoglasnika i, izgovorenog od muškog govornika (LRR),
metodom kovarijance odnosno autokorelacijskom metodom (s Hamming-ovim
vremenskim otvorom). Na slikama se vidi da signal predikcijske pogreške ima
oštar puls na početku svakog pitch perioda a pripadajući spektar je dosta
ravan, ali pokazuje efekt češlja zbog periodičnosti pobudnog signala. Treba
primijetiti veliku predikcijsku pogrešku na početku segmenta, na slici 9.10‑3, analiziranog autokorelacijskom metodom. Do velikog
iznosa pogreške dolazi zbog toga što se pokušava predvidjeti uzorke signala
različitih od nule na osnovi nuliranih uzoraka lijevo od intervala 
. Oblik Hammingovog vremenskog otvora s prigušenjem prema
rubovima nije potpuno učinkovit pri smanjenju te pogreške.
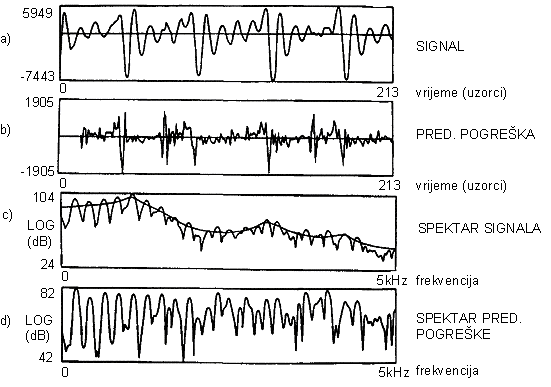
Slike 9.10‑4 i 9.10‑5 prikazuju slične rezultate za 20 ms samoglasnika a, izgovorenog od ženske govornice. Unutar analiziranog intervala nalazi se oko pet kompletnih pitch perioda. Tako na slici 9.10‑4 signal pogreške ima velik broj oštrih vrhova u intervalu analize metodom kovarijance. Međutim, korištenjem Hammingovog vremenskog otvora u autokorelacijskoj metodi dolazi do smanjivanja amplitude pitch pulseva na rubovima analiziranog intervala, pa su stoga i vrhovi u signalu predikcijske pogreške smanjene amplitude prema rubovima.
|
Slika |
Tipični signali i spektri za LPC metodu kovarijance, za žensku govornicu, p = 14, N = 200 |
|
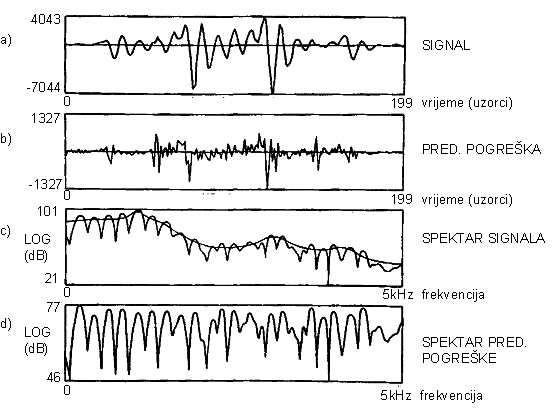
Slika |
Tipični signali i spektri za LPC autokorelacijsku metodu sa Hamming-ovim vremenskim otvorom, za žensku govornicu, p = 14, N = 200 |
Promatrajući ponašanje signala predikcijske pogreške prikazanog na prethodnim slikama 9.10‑2 do 9.10‑5, može se doći do zaključka da je signal predikcijske pogreške dobar kandidat za signal iz kojeg bi se mogao jednostavno odrediti pitch period. Na nesreću, situacija nije tako čista za druge primjere zvučnog govora. Makhoul i Wolf su pokazali da za glasove koji nisu bogati harmonicima, npr. likvide kao r, l ili nazale kao m,n, vrhovi u signalu predikcijske pogreške nisu uvijek jako oštri ili jasno vidljivi. Osim toga, na spoju između zvučnih i bezvučnih glasova oznake periodičnosti u signalu predikcijske pogreške često potpuno nestanu.
Na kraju, iako se signal predikcijske pogreške 
čini idealnim
kandidatom za detekciju pitch perioda, postoje teškoće pri lociranju glotalnih
pulseva za mnoštvo zvučnih glasova, pa se stoga u ovoj primjeni ne može potpuno
osloniti samo na signal predikcijske pogreške.
1.2 Izrazi za predikcijsku pogrešku
Normalizirana srednja kvadratna predikcijska pogreška za autokorelacijsku metodu je definirana kao:
|
|
gdje je 
izlaz filtra
predikcijske pogreške koji odgovara segmentu govora 
pozicioniranom na
vremenskom indeksu n. Za metodu kovarijance odgovarajuća
definicija je:
|
|
Ako definiramo 
, niz predikcijske pogreške može se izraziti kao:
|
|
Uvrštenjem jednadžbe (9.11‑3) u jednadžbe (9.11‑1) ili (9.11‑2) (ovisno o korištenoj metodi) i koristeći izraz (9.3‑19), slijedi:
|
|
a uvrštenje (9.3‑20) u (9.11‑4) daje:
|
|
Drugi izraz za 
dobiven je Durbinovim
algoritmom, to jest:
|
|
Gornji izrazi nisu svi ekvivalentni i mogu biti tumačeni ovisno o detaljima korištene metode linearne predikcije. Na primjer, jednadžba (9.11‑6) bazirana je na Durbinovom algoritmu i vrijedi samo za autokorelacijsku i lattice metodu. Nadalje, pošto lattice metoda eksplicitno ne zahtijeva računanje korelacijske funkcije, jednadžbe (9.11‑4) i (9.11‑5) nisu direktno primjenjive na lattice metodu. U tabeli 9.11‑1 sažeti su gornji izrazi za normaliziranu srednju kvadratnu pogrešku predikcije i prikazana je valjanost izraza za pojedinu metodu.
|
Izraz za predikcijsku pogrešku |
Metoda |
Autokorelacijska |
Lattice |
|
|
vrijedi |
vrijedi* |
vrijedi |
|
|
vrijedi |
vrijedi** |
ne vrijedi |
|
|
vrijedi |
vrijedi** |
ne vrijedi |
|
|
ne vrijedi |
vrijedi |
vrijedi |
* ..... u slučaju da 
predstavlja segment
signala pomnožen s vremenskim otvorom
** ... u slučaju da se 
zamijeni sa 